5. C modeling

5.1. Characteristics of modeling

In this modeling, we validate the use of the macro-command MACR_ECREVISSE in relation to rotation and translation. So it is not a non-regression test.

Indeed, Crayfish results depend only on the characteristics of the crack, including the direction. It is influenced by gravity. Thus, cracks with the same characteristics and having a symmetric direction with respect to the vertical must give the same flows.

We work with the same parameters (of the material, of the flow of the crack) as in modeling A (§ 1.1). The mesh is also the same except that it is rotated and translated. Details of the mesh are given in §5.2.

5.2. Meshing and boundary conditions.

The two meshes used were obtained by rotation and translation of the modeling A mesh, so they maintain the same dimensions. They are featured in the and.

For the first mesh, the first curvilinear abscissa of the crack is the point of origin of the \((0;0)\) axes.

The second mesh results from a 120 degree rotation of the first mesh around the origin and a translation of vector \((\mathrm{-}10;20)\).

The boundary conditions for both meshes are analogous to modeling A:

1. The sides named FIXE1 (or FIXE2) are embedded (\(\mathit{DX}\mathrm{=}0\), \(\mathit{DY}\mathrm{=}0\)).

2. A contact condition is defined between lips BFISH1 - BFISB1 (BFISH2 - BFISB2) (DEFI_CONTACT).

3. The pressure and the temperature on the intrados INTRA1 (INTRA2) are greater than on the extrados EXTRA1 (EXTRA2): (\(1.E6\mathrm{Pa}\) and \(140°C\) versus \({P}_{\mathrm{atm}}\) and \(20°C\)). This causes the flow from the intrados to the extrados.

4. At the beginning of the calculation, the material is considered to be at ambient temperature \(20°C\), which is the reference temperature.

Figure 5.2-a : Mesh 1 for the direction \(\mathit{theta}\mathrm{=}120°\) (compared to the vertical) .

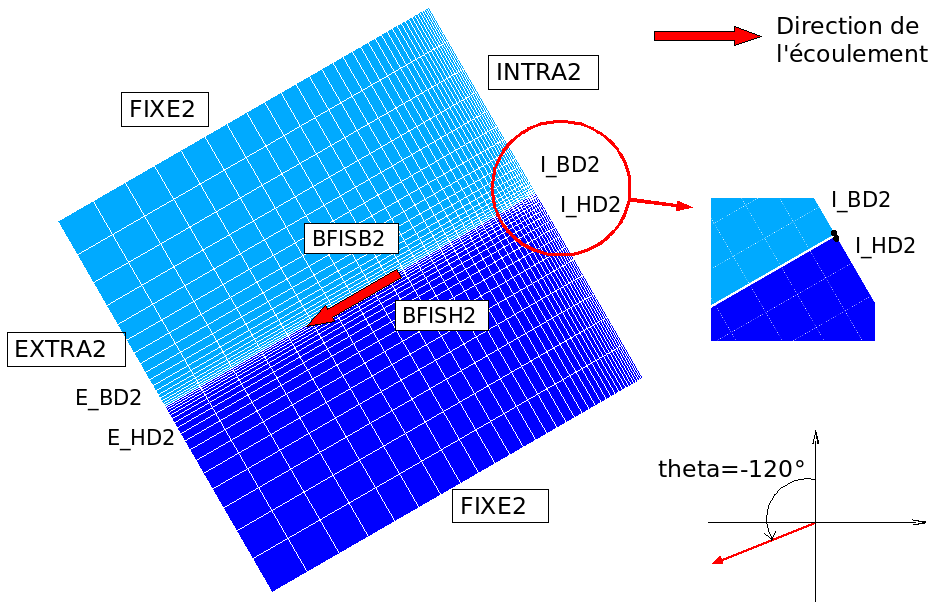
Figure 5.2-b : Mesh 2 for the direction \(\mathit{theta}\mathrm{=}\mathrm{-}120°\) (compared to the vertical) .

5.3. Tested sizes and results

We’re testing the results at moment \(t=10000s\). The values of the result of mesh 2 are extracted, and they are compared to those corresponding to mesh 1.

Mesh 1	Mesh 2
Move \(\mathit{DX}\) to node \({E}_{\mathit{HD1}}\)	by symmetry: (-1) * Move \(\mathit{DX}\) to node \({E}_{\mathit{BD2}}\)
Move \(\mathit{DX}\) to node \({E}_{\mathit{BD1}}\)	by symmetry: (-1) * Move \(\mathit{DX}\) to node \({E}_{\mathit{HD2}}\)
Move \(\mathit{DY}\) to node \({E}_{\mathit{HD1}}\)	by symmetry: Move \(\mathit{DY}\) to node \({E}_{\mathit{BD2}}\)
Move \(\mathit{DY}\) to node \({E}_{\mathit{BD1}}\)	by symmetry: Move \(\mathit{DY}\) to node \({E}_{\mathit{HD2}}\)
Material temperature at node \({I}_{\mathit{HD1}}\)	Material temperature at node \({I}_{\mathit{HD2}}\)
Total flow	Total flow
Convection coefficient first abs. curv.	Convection coefficient first abs. curv.
First pressure abs. curv.	First pressure abs. curv.
Primary fluid temperature abs. curv.	Primary fluid temperature abs. curv.
Fluid heat flow first abs. curv.	Fluid heat flow first abs. curv.

Size	Tolerance
Move \(\mathit{DX}\) at nodes \({E}_{\mathit{HD1}}\)	1.0E-05
Move \(\mathit{DX}\) to node \({E}_{\mathit{BD1}}\)	1.0E-05
Move \(\mathit{DY}\) to node \({E}_{\mathit{HD1}}\)	1.0E-05
Move \(\mathit{DY}\) to node \({E}_{\mathit{BD1}}\)	1.0E-05
Material temperature at node \({I}_{\mathit{HD1}}\)	1.0E-04
Total flow	1.0E-03
Convection coefficient first abs. curv.	1.0E-04
First pressure abs. curv.	1.0E-04
Primary fluid temperature abs. curv.	1.0E-04
Fluid heat flow first abs. curv.	1.0E-03

5.4. notes

The lips are in contact, the DEFI_CONTACT command is activated. The flow calculation is carried out with the residual opening.