4. B modeling#
4.1. Characteristics of modeling#
In this modeling, we validate the use of the macro command MACR_ECREVISSE in the presence of 2 vertical cracks. The geometry is slightly different from that of modeling A. It is described with the mesh in. The characteristics of the flow and of the material were described in § 1.
As for modeling A, we work with plane deformations for mechanics (D_ PLAN), and with a diagonalized mass matrix for thermal (PLAN_DIAG).
4.2. Meshing and boundary conditions#
The mesh used is shown:
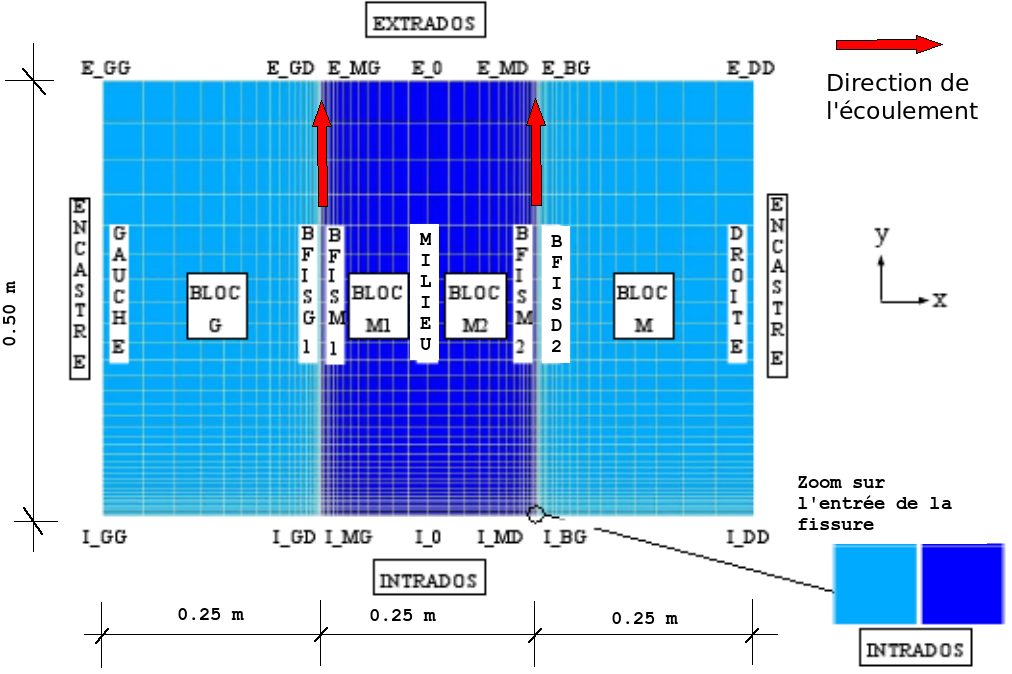
Figure 4.2-a : Full mesh
The dimensions of each of the three blocks are \(0.50m\) high and \(0.25m\) wide.
Number of knots: 2275
Number of stitches: 2108 QUAD4
The growth parameters for the mesh sizes used to create the mesh are as follows: from \(0.002m\) (intrados) to \(0.05m\) (extrados), and idem from BFISG1/BFISD2 to ENCASTRE; from \(0.025m\) to MILIEU to \(0.002m\) to on BFISM1/BFISM2.
The cracks are named after the lips: BFISG1 - BFISM1 (FISSURE 1), (FISSURE 2).
Boundary conditions:
The sides named ENCASTRE are embedded (\(\mathit{DX}\mathrm{=}0\), \(\mathit{DY}\mathrm{=}0\)).
On side MILIEU (line of symmetry) the movement in the direction \(X\) (\(\mathit{DX}\mathrm{=}0\)) is blocked.
A contact condition is defined between lips BFISG1 - BFISM1 and BFISM2 - BFISD2 (DEFI_CONTACT).
The pressure and temperature on the intrados INTRADOS are greater than on the extrados EXTRADOS (\(1.E6\mathrm{Pa}\) and \(140°C\) versus \(1.E6\mathrm{Pa}\) and \(20°C\)), which causes the flow from the intrados to the extrados.
At the beginning of the calculation, the material is considered to be at room temperature \(20°C\), which is the reference temperature.
4.3. Sizes and results#
At 2 different times, the displacements and the temperature at the entrance of the left crack and at the exit of the right crack are tested. Finally, we test the flow of the crack on the right at \(t=500s\) and the crack on the left at \(t=10000s\).
At \(t=500s\):
Identification |
Tolerance |
Move \(\mathit{DX}\) to node \({E}_{\mathit{MD}}\) \(\mathrm{[}m\mathrm{]}\) |
1.0E-06 |
Material temperature at node \({E}_{\mathit{MD}}\) \(\mathrm{[}°C\mathrm{]}\) |
1.0E-06 |
Displacement \(\mathit{DX}\) node \({I}_{\mathit{GD}}\) \(\mathrm{[}m\mathrm{]}\) |
1.0E-06 |
Material temperature at node \({I}_{\mathit{GD}}\) \(\mathrm{[}°C\mathrm{]}\) |
1.0E-06 |
Fissure BFISG1 - BFISM1, flow |
1.0E-06 |
At \(t=10000s\):
Identification |
Tolerance |
Move \(\mathit{DX}\) to node \({E}_{\mathit{MD}}\) \(\mathrm{[}m\mathrm{]}\) |
1.0E-06 |
Material temperature at node \({E}_{\mathit{MD}}\) \(\mathrm{[}°C\mathrm{]}\) |
1.0E-06 |
Move \(\mathit{DX}\) to node \({I}_{\mathit{GD}}\) \(\mathrm{[}m\mathrm{]}\) |
1.0E-06 |
Material temperature at node \({I}_{\mathit{GD}}\) \(\mathrm{[}°C\mathrm{]}\) |
1.0E-06 |
Fissure BFISM2 - BFISD2, flow |
1.0E-06 |
4.4. notes#
The crack opening at \(t=10000s\) is of the order of \({10}^{-9}\), so it is almost closed due to thermal expansion due to the high temperature below. In this case too, it is the residual opening that is used to calculate the flow.