3. Application examples#

3.1. Presentation#

The example used to present the implementation of parametric studies is shown in the figure below. It is a beam that is embedded at one end and subjected to distributed pressure at the other end. The objective of this parametric study is to determine the evolution of the equivalent Von Mises stress along the upper line of the beam as a function of orientation \(\mathrm{\alpha }\).

The data files are those from the distr01a test case.

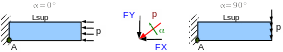
The calculations will be done every \(22.5°\), for an angle \(\mathrm{\alpha }\) varying from \(0°\) to \(90°\). The number of calculation scenarios to be carried out is therefore 5. In the table below we present the values that the parameters \(\mathit{FX}\) and \(\mathit{FY}\) go successively.

Scenario no.	Angle \(\mathrm{\alpha }\)	\(\mathit{FX}=P\mathrm{.}\mathrm{cos}(a)\)	\(\mathit{FY}=P\mathrm{.}\mathrm{sin}(a)\)
1	0.0°	\({10}^{6}\)	\(0.\)
2	22.5°	\(9.23879\times {10}^{5}\)	\(-3.82683\times {10}^{5}\)
3	45.0°	\(7.07106\times {10}^{5}\)	\(-7.07106\times {10}^{5}\)
4	67.5°	\(3.82683\times {10}^{5}\)	\(-9.23879\times {10}^{5}\)
5	90.0°	\(0.\)	\(-{10}^{6}\)

Table 3.1-1: Parameter values

The nominal study order file is distr01a.comm.

In the rest of this presentation, we will detail the implementation of this type of calculation, namely:

the generation of the “distr” file
the use of parameters in the command file.

3.2. Definition of the parameter set and calculation cases#

It is possible to define the parameters in the “.distr” file in two ways:

Explicitly: in this case the user provides all the values that the parameters can take.
Calculated: in this case the user uses Python programming
- to automatically calculate these parameters in conditional form or not,
- to automatically define these calculation scenarios, for example by scanning all possible combinations of parameters or by choosing the min/mean/max values of the parameters.

3.2.1. Explicit “distr” file#

In this case, the values of the parameters are explicitly written in the “distro” file. In the case of the example, it is in the following form (file distr01a.50 from the test case):

VALE =(

_F (F_Norm=1.E6, F_Tang=0.), # calculation case 1

_F (F_Norm=9.23879E5, F_Tang=-3.82683E5), # calculation case #2

_F (F_Norm=7.07106E5, F_Tang=-7.07106E5), # calculation case #3

_F (F_Norm=3.82683E5, F_Tang=-9.23879E5), # calculation case #4

_F (F_Norm=0., F_Tang=-1.E6), # calculation case no. 5

)

Figure 3.2.1-a :: **File’distr”explicit

3.2.2. Calculated “distr” file#

In this case, writing the “distr” file is less simple, we use Python programming. For this example, it takes the following form (file distr01a.51 from the test case):

From math import pi, cos, sin

Numpy import

VALE = []

n = 5

list_theta = numpy.arange (n) *22.5* pi/180.

P = 1.e6

For a in list_theta:

VALE .append (_F (F_Norm = P*cos (a),

F_Tang = P*sin (a),))

Figure 3.2.2-a : File “distr” calculated

3.3. Using parameters in the command file#

All you have to do is reference, in the nominal command file, the names of the parameters present in the “distro” file.

DEBUT ()

# Initialization (here the values of the parameters will appear)

F_Norm=0.

F_Tang=0.

...

CHAR = AFFE_CHAR_MECA (MODELE = MODE,

FORCE_CONTOUR =_F (GROUP_MA = 'Press',

FX = F_Norm,

FY=F_Tang),)

3.4. Post-treatments#

The file distr01a.11 gives an example of post-processing with rereading all the result files, merging the results into a single table, printing a curve with all the changes in the constraint…