1. Stability of a conservative system#
1.1. Definition of the stability of a conservative system#
The equilibrium position of a conservative system is said to be stable if it is invariant under the effect of small disturbances. This amounts to verifying that the solution obtained is indeed located on a local minimum of potential energy or in other words, verifying that the Hill functional [bib19] is convex. Mathematically, this results in verifying the positivity of the second derivative of the potential energy Φ at the equilibrium point u. Let us consider a small disturbance in the equilibrium state v, respecting the boundary conditions imposed on the structure. We must always find inequality:
\(\phi (u)\mathrm{\le }\phi (u+v)\) eq 1.1‑1
The main cause of loss of stability for a conservative mechanical structure is buckling. We will therefore be more particularly interested in this concept in the future.
Note: There are other definitions of stability. In particular, we find stability in the meaning of Rice, a criterion defined in 1975, which amounts to verifying the strict positivity of the eigenvalues of the acoustic tensor. However, one can have instability in the sense of Hill before instability in the sense of Rice. The criterion in Hill’s sense is therefore more conservative. That is why it is the one we prefer.
1.2. General concept of buckling#
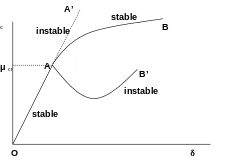
Buckling is a phenomenon of instability [bib6]. Its appearance can be observed in particular on slender elements with low flexural stiffness. Beyond a certain load level, the structure undergoes a major change in configuration (which may result in the sudden appearance of undulations, for example). There are two types of buckling: buckling by bifurcation and buckling by limit point ([bib1], [bib7], [bib8]). To describe the behavior of these two types of buckling, we consider a structure whose parameter \(\mu\) is characteristic of the load and whose parameter \(\delta\) is characteristic of the displacement is considered.
|
Figure 1.2-a : Buckle by bifurcation
Between point \(O\) and point \(A\), the structure admits a single family of curve \((\mu ,\delta )\). For example, it can be classical linear elasticity or elastoplasticity, where if the problem is well posed (cf. [§ 1.3]), we have the classic result of existence and uniqueness of the solution. On the other hand, beyond point \(A\), several families of curves are solutions to the balance problem. This loss of uniqueness is accompanied by instability in the initial branch (called fundamental). The secondary branch can be stable (curve \(\mathit{AB}\)) or unstable (curve \(\mathit{AB}’\)). The load beyond which there is a bifurcation is called critical load \({\mu }_{\mathit{cr}}\). Buckling by bifurcation is characterized by the fact that the mode (or direction of buckling), which initiates the secondary branch, does not generate additional work in the load applied: the buckling mode being orthogonal to it.
An example of buckling by bifurcation with instability of the secondary branch is found in the case of a circular cylindrical shell under axial compression [bib10]. Examples of buckling by bifurcation with secondary branch stability are found in elastic beams under axial compression, circular rings under radial compression, and rectangular plates under longitudinal compression.
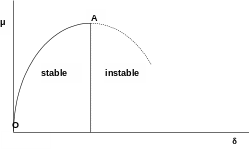
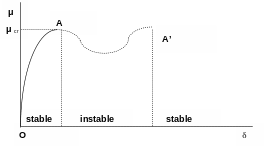
|
Figure 1.2-b : Buckling by limit point
Figure 1.2-c : Buckling by limit point with breakdown
In figures [Figure 1.2-b] and [Figure 1.2-c], which illustrate buckling by limit point, the structure admits only one family \((\mu ,\delta )\) of solutions of equilibrium equations. At point \(A\), there is a loss of stability of the solution with total loss of stiffness in the case of figure [Figure 1.2-b] and with a breakdown phenomenon in the case of figure [Figure 1.2-c] (the solution becomes stable again after a discontinuity of movement; case of a spherical shell under external pressure). Point \(A\) is then called the limit point. In all cases, the problem therefore comes down to looking for the load at which the fundamental branch of equilibrium becomes unstable or whose stability is uncertain. This generally involves major trips. Finally, we can have the case of ruin by plastic flow, which is similar to the limit point [Figure 1.2-b].
Code_Aster allows the search for linear buckling modes, called an Euler method. All you have to do is solve a generalized eigenvalue problem (using the CALC_MODES operator with the keyword TYPE_RESU =” MODE_FLAMB “). The two argument matrices of the generalized problem are the stiffness matrix and the geometric rigidity matrix, resulting from a prior linear elastic calculation (operator MECA_STATIQUE).
In all cases where nonlinearities, whether geometric or behavioral, cannot be overlooked, the Euler approach is no longer valid.
We therefore propose an ad hoc criteria, which can be considered as a generalization of the Euler criterion on an updated configuration. This criterion is built on the assembled tangent stiffness matrix, which is calculated in the Newtons-type algorithm to solve nonlinear (operator STAT_NON_LINE) or dynamic non-linear transient problems (operator DYNA_NON_LINE). This nonlinear criterion makes it possible to rigorously treat nonlinear elastic behavior relationships. On the other hand, laws that have a dissipative aspect are treated rigorously only if the loading, at any point in the structure, follows a monotonic evolution (this corresponds to Hill’s hypothesis [bib4]).
1.3. Writing the mechanical problem#
The objective of this chapter is to introduce the general structure calculation formalism adapted to the nonlinear mechanical problem that we want to address.
To begin with, we will therefore briefly recall the equation of a typical structural calculation problem. To simplify, we place ourselves, at least at the beginning, in the context of small disturbances.

|
Figure 1.3-a : Representation of a structural calculation problem
The structure \({\Omega }_{S}\) is subject to imposed volume forces \({\mathrm{f}}_{d}\), surface forces \({F}_{d}\) on the edge \(\partial {\Omega }_{S2}\) and imposed displacements \({U}_{d}\) on the rest of the edge of \({\Omega }_{S}\), noted \(\partial {\Omega }_{S1}\).
The unknowns of the reference problem on the solid are the field of displacement
and the Cauchy \(\sigma\) constraint field.
The solution (\(u,\sigma\)) of the structure problem where thermal effects are neglected is defined as:
Find \((u,\sigma )\in {H}_{1}({\Omega }_{S})\times {L}^{2}({\Omega }_{S})\) who checks:
Connection equations:
\(\mathrm{u}{\mathrm{\mid }}_{\mathrm{\partial }{\Omega }_{S1}}\text{=}{\mathrm{U}}_{\mathrm{d}}\) eq 1.3‑1
Behavioral relationship:
\(\sigma \text{=}f(\varepsilon )\) with \(\varepsilon\) which is the strain tensor eq 1.3‑2
\(\varepsilon \text{=}\frac{1}{2}(\mathrm{\nabla }\mathrm{u}\text{+}\mathrm{\nabla }{\mathrm{u}}^{\mathrm{T}})\) in the hypothesis of small disturbances eq 1.3‑3
Assuming linear elastic behavior
\(\sigma \text{=}\mathrm{C}\text{:}\varepsilon\) eq 1.3‑4
Equations of balance:
\(\{\begin{array}{c}\rho \gamma \text{=}\nabla \text{.}\sigma \text{+}{f}_{d}\text{avec}\gamma \text{=}\frac{{\text{d}}^{2}u}{\text{d}{t}^{2}}\\ \sigma \text{.}n{\mid }_{\partial {\Omega }_{S2}}\text{=}{F}_{d}\end{array}\) eq 1.3‑5
1.4. Stability study#
The purpose of this chapter is to present methods for determining the stability of the nonlinear quasistatic equilibrium of a structure in a conservative system. To begin with, we are only interested in the detection of instability, or more exactly in the loss of uniqueness of the solution [bib6]. Recent synthesis studies include [bib9] or [bib7] or [] and [bib8], which present very comprehensive papers on the analysis of nonlinear stability of structures.
The calculation of the post-critical solution will not be discussed.
To do the stability analysis, we are introducing an initial reference configuration \({\Omega }_{S0}\), a current configuration \({\Omega }_{S}\), and a disturbed configuration \({\Omega }_{S1}\):
OHS1 ΩS OHM S0 α u 1 u 0 u |
Figure 1.4-a : Definition of the different configurations
Let \(u\) be the field for moving the points in the structure. For the time being, the behavior is assumed to be linear elastic isotropic. The structure subjected to the movements and forces imposed will deform and become the structure identified by the current configuration \({\Omega }_{S}\). We seek to determine a state of equilibrium characterized by the field of displacement between the initial configuration \({\Omega }_{S0}\) and the current configuration \({\Omega }_{S}\), as well as a Cauchy constraint field, noted \(\sigma\), or Piola-Kirchhoff II, noted \(\pi\):
\(\pi \text{=}\text{det}F\text{.}{F}^{\text{-}1}{\pi }_{I}\) with \(\{\begin{array}{c}F\text{=}\nabla u\text{+}I\text{: tenseur gradient de la transformation}\\ \text{det}F\text{=}\frac{{\rho }_{0}}{\rho }\\ {\pi }_{I}\text{: tenseur de Piola - Kirchhoff I}\end{array}\) \(\Rightarrow \pi \text{=}\frac{{\rho }_{0}}{\rho }\text{.}{F}^{\text{-}1}\text{.}\sigma \text{.}{F}^{\text{-}T}\) eq 1.4‑1
In this expression, we see the relationship between the initial density \({\rho }_{0}\) and the current density \(\rho\) appear.
The next step is to predict the stability of this balance.
To this end, we are going to look for a criterion to determine if there is a single field of movement that balances the forces applied. We will assume that the efforts are gradually increasing and we will try to find out when there are two configurations \({\Omega }_{S}\) and \({\Omega }_{S1}\) that respect the equations of the problem: we are looking for a bifurcation point, that is to say a loss of uniqueness of the solution. This moment will be described as an instant of buckling.
1.4.1. Writing the elastic geometric nonlinear problem#
Solution \(\mathrm{u},\pi\) of the structure problem without thermal effects verifies ([bib1], [bib7], [bib2]):
Connection equations:
\(u{\mid }_{\partial {\Omega }_{S0}}\text{=}{U}_{d}\) eq 1.4.1-1
Elastic behavior relationship:
\(\pi \text{=}{\varphi }_{\text{,}\varepsilon }(\varepsilon )\) eq 1.4.1-2
with \(\varepsilon\) which is the strain tensor. Assuming linear elastic behavior:
\(\pi \text{=}\mathrm{C}\varepsilon\) eq 1.4.1-3
Equations of balance:
\(\mathrm{\{}\begin{array}{c}\rho \underline{\gamma }\text{=}\mathrm{\nabla }\text{.}\pi \text{+}{\mathrm{f}}_{d}\text{avec}\gamma \text{=}\frac{{\text{d}}^{2}\mathrm{u}}{\text{d}{t}^{2}}\\ \mathrm{F}\text{.}\pi \text{.}{\mathrm{n}}_{0}{\mathrm{\mid }}_{\mathrm{\partial }{\Omega }_{S0}}\text{=}{\mathrm{F}}_{d}\end{array}\) eq 1.4.1-4
The associated deformation tensor is that of Green-Lagrange (referenced to the initial configuration):
\(\begin{array}{}\varepsilon (u)\text{=}\frac{1}{2}({F}^{T}F\text{-}I)\text{avec}F\text{=}\nabla u\text{+}I\\ \Rightarrow \varepsilon (u)\text{=}{\varepsilon }^{L}(u)\text{+}\frac{1}{2}{\varepsilon }^{Q}(u,u)\end{array}\) eq 1.4.1-5
with: \(\mathrm{\{}\begin{array}{c}{\varepsilon }^{L}(\mathrm{u})\text{=}\frac{1}{2}(\mathrm{\nabla }\mathrm{u}\text{+}{\mathrm{\nabla }}^{T}\mathrm{u})\text{: partie linéaire}\\ {\varepsilon }^{Q}(\mathrm{u},\mathrm{u})\text{=}{\mathrm{\nabla }}^{T}\mathrm{u}\text{.}\mathrm{\nabla }\mathrm{u}\text{: partie quadratique}\end{array}\) eq 1.4.1-6
We can now write the Principle of Virtual Powers in geometric nonlinear elasticity and in quasistatics:
\({p}^{\mathrm{intal}\text{int}}\text{-}{p}^{\mathrm{ext}}\text{=}\mathrm{0,}\forall {u}^{\text{*}}\text{C A 0}\)
\(\text{Avec :}\{\begin{array}{c}{p}^{\text{int}}\text{=}\underset{{\Omega }_{S0}}{\int }\mathrm{Tr}(\pi {\varepsilon }^{\text{*}})d\Omega \text{=}\underset{{\Omega }_{S0}}{\int }\mathrm{Tr}\left[({\varepsilon }^{L}(u)\text{+}\frac{1}{2}{\varepsilon }^{Q}(u,u))C({\varepsilon }^{L}({u}^{\text{*}})\text{+}{\varepsilon }^{Q}(u,{u}^{\text{*}}))\right]d\Omega \\ {p}^{\text{ext}}\text{=}\underset{\partial {\Omega }_{S0}}{\int }{F}_{d}\text{.}{u}^{\text{*}}\mathrm{dS}\text{+}\underset{{\Omega }_{S0}}{\int }{f}_{d}\text{.}{u}^{\text{*}}d\Omega \end{array}\) eq 1.4.1-7
In order to obtain a discretized formulation, the deformation tensor can be rewritten:
\(\{\begin{array}{c}\varepsilon (u)\text{=}\left[{B}^{L}\text{+}\frac{1}{2}{B}^{\mathrm{NL}}(u)\right]\text{.}u\\ \pi \text{=}C\varepsilon (u)\text{avec}\pi \text{qui est le tenseur de Piola - Kirchhoff II}\end{array}\) eq 1.4.1-8
The power of internal efforts becomes:
\({\mathrm{P}}^{\text{int}}\text{=}\underset{{\Omega }_{SO}}{\mathrm{\int }}\mathit{Tr}\left[\pi \text{.}{\mathrm{[}{\mathrm{B}}^{\mathrm{L}}\text{+}{\mathrm{B}}^{\mathrm{NL}}(\mathrm{u})\mathrm{]}}^{T}{\mathrm{u}}^{\text{*}}\right]d\Omega\) eq 1.4.1-9
Taking into account the behavioral relationship [éq 1.4.1-3]:
\({\mathrm{P}}^{\text{int}}\text{=}\underset{{\Omega }_{S0}}{\mathrm{\int }}\mathit{Tr}\left[{\mathrm{[}{\mathrm{B}}^{\mathrm{L}}\text{+}\frac{1}{2}{\mathrm{B}}^{\mathrm{NL}}(\mathrm{u})\mathrm{]}}^{T}\mathrm{C}\mathrm{[}{\mathrm{B}}^{\mathrm{L}}\text{+}{\mathrm{B}}^{\mathrm{NL}}(\mathrm{u})\mathrm{]}\mathrm{u}\text{.}{\mathrm{u}}^{\text{*}}\right]d\Omega\) eq 1.4.1-10
After discretization by the finite elements, we can put this equation in matrix form:
\({u}^{\text{*}}\text{.}[{K}_{0}\text{+}{K}^{L}(u)\text{+}{K}^{Q}(u)]\text{.}u\text{=}{P}^{\mathrm{ext}}\) eq 1.4.1-11
The matrix \({\mathrm{K}}^{\mathrm{L}}\) is symmetric and we have the following expressions:
\(\{\begin{array}{c}{K}_{0}\text{=}\underset{{\Omega }_{S0}}{\int }{B}^{{L}^{T}}C{B}^{L}d\Omega \\ {K}^{L}\text{=}\underset{{\Omega }_{S0}}{\int }\left[\frac{1}{2}{B}^{\mathrm{NL}}{(u)}^{T}C{B}^{L}\text{+}{B}^{{L}^{T}}C{B}^{L}(u)\right]d\Omega \\ {K}^{Q}\text{=}\frac{1}{2}\underset{{\Omega }_{S0}}{\int }{B}^{\mathrm{NL}}{(u)}^{T}C{B}^{\mathrm{NL}}d\Omega \end{array}\) eq 1.4.1-12
We obtain directly from the above the writing in matrix form of the balance:
\([{K}_{0}\text{+}{K}^{L}(u)\text{+}{K}^{Q}(u)]\text{.}u\text{=}{F}^{\mathrm{ext}}\) eq 1.4.1-13
Or again, in an equivalent manner:
\({F}^{\text{int}}\text{=}{F}^{\mathrm{ext}}\text{avec}{F}^{\text{int}}\text{=}\underset{{\Omega }_{S0}}{\int }{[{B}^{L}\text{+}{B}^{\mathrm{NL}}(u)]}^{t}\pi d\mathrm{OMEGA}\) eq 1.4.1-14
We can just as easily formulate the Principle of Virtual Powers from the Cauchy stress state and the Almansi deformation tensor (therefore on the current configuration). We then obtain:
\(\underset{{\Omega }_{S}}{\int }\mathrm{Tr}(\sigma \varepsilon ({u}^{\text{*}}))d\Omega \text{=}\underset{\partial {\Omega }_{S}}{\int }{F}_{d}\text{.}{u}^{\text{*}}\mathrm{dS}\text{+}\underset{{\Omega }_{S}}{\int }{f}_{d}\text{.}{u}^{\text{*}}d\Omega\) eq 1.4.1-15
Which can also be put in the following form, after discretization:
\(\underset{{\Omega }_{S}}{\int }{B}^{T}\sigma d\Omega \text{=}{F}^{\text{int}}\text{=}{F}^{\mathrm{ext}}\) eq 1.4.1-16
Or again, assuming the elastic behavior relationship:
\(Ku\text{=}{F}^{\mathrm{ext}}\text{avec}K\text{=}\underset{{\Omega }_{S}}{\int }{B}^{T}CBd\Omega\) eq 1.4.1-17
The integrals of these equations are calculated on the current volume \({\Omega }_{S}\) which depends, of course, on the displacement field solution \(u\). Likewise, the operator \(B\) must be calculated on the current configuration \({\Omega }_{S}\) and not on the initial configuration \({\Omega }_{S0}\), as was the case previously.
1.4.2. Geometric nonlinear stability study#
We are going to find out if there is a second kinematically admissible field of displacement that verifies the equilibrium equations: we therefore want to know if we will bifurcation.
This second field will be written as the sum of a disturbance added to the first solution, i.e.: \(u\text{=}\alpha {u}_{1}\), with \(\alpha\) which is a very small real and which we will make tend towards 0. Field \({u}_{1}\) is chosen kinematically admissible at 0.
The Principle of Virtual Powers will then be written for this new field.
The deformation field takes the form:
\(\varepsilon (u\text{+}\alpha {u}_{1})\text{=}\varepsilon (u)\text{+}\alpha \left[{\varepsilon }^{L}({u}_{1})\text{+}\frac{1}{2}({\varepsilon }^{Q}({u}_{1},u))\right]\text{+}\frac{{\alpha }^{2}}{2}{\varepsilon }^{q}({u}_{1},{u}_{1})\) eq 1.4.2-1
The virtual deformations are given by:
\({\varepsilon }_{1}^{\text{*}}\text{=}{\varepsilon }^{L}({u}^{\text{*}})\text{+}{\varepsilon }^{q}(u,{u}^{\text{*}})\text{+}\alpha {\varepsilon }^{Q}({u}_{1},{u}^{\text{*}})\text{=}\varepsilon ({u}^{\text{*}})\text{+}\alpha {\varepsilon }^{Q}({u}_{1},u)\) eq 1.4.2-2
Likewise, if we choose \({\Omega }_{\mathrm{S0}}\) as the reference configuration, the constraints become:
\({\pi }_{1}\text{=}\pi \text{+}\alpha C\left[{\varepsilon }^{L}({u}_{1})\text{+}\frac{1}{2}({\varepsilon }^{Q}(u,{u}_{1})\text{+}{\varepsilon }^{Q}({u}_{1},u))\right]\text{+}\frac{{\alpha }^{2}}{2}C{\varepsilon }^{Q}({u}_{1},{u}_{1})\) eq 1.4.2-3
We can now express the Principle of Virtual Powers for the disturbed field of movement. Let us assume that the forces imposed do not depend on the displacement and that the initial configuration is chosen as a reference.
\(\{\begin{array}{c}{P}_{1}^{\text{int}}\text{=}{P}^{\text{int}}\\ \text{+}\alpha \left[\underset{{\Omega }_{\mathrm{S0}}}{\int }\mathrm{Tr}(\pi {\varepsilon }^{Q}({u}_{1},{u}^{\text{*}}))d\Omega \text{+}\underset{{\Omega }_{\mathrm{S0}}}{\int }\mathrm{Tr}\left[\varepsilon ({u}^{\text{*}})C({\varepsilon }^{L}({u}_{1})\text{+}\frac{1}{2}({\varepsilon }^{Q}(u,{u}_{1})\text{+}{\varepsilon }^{Q}({u}_{1},u)))\right]d\Omega \right]\text{+}o(\alpha )\\ {P}_{1}^{\text{ext}}\text{=}{P}^{\text{ext}}\\ {P}_{1}^{\text{int}}\text{-}{P}_{1}^{\text{ext}}\text{=}0\end{array}\) eq 1.4.2-4
For \(\alpha\) small enough, it will suffice for the term proportional to \(\alpha\) in the expression [éq 1.4.2-4] to be zero for the Principle of Virtual Powers to be verified for the field \(u\text{=}\alpha {u}_{1}\). In this case, there will therefore no longer be the uniqueness of the solution, which will result in the loss of system stability.
When the forces imposed do not depend on the geometric configuration, the stability study is therefore expressed as:
Knowing the current state, i.e. the displacement field \(u\) kinematically admissible and the constraint field \(\pi\), if there is a displacement field \({u}_{1}\) kinematically admissible to 0 and such that, for any movement \({u}^{\text{*}}\) kinematically admissible to 0, we have: \(\begin{array}{c}\underset{{\Omega }_{\mathit{S0}}}{\mathrm{\int }}\mathit{Tr}(\pi {\varepsilon }^{Q}({\mathrm{u}}_{1},{\mathrm{u}}^{\text{*}}))d\Omega \\ \text{+}\underset{{\Omega }_{\mathit{S0}}}{\mathrm{\int }}\mathit{Tr}\left[{\varepsilon }^{L}({\mathrm{u}}^{\text{*}})\mathrm{C}{\varepsilon }^{L}({\mathrm{u}}_{1})\text{+}{\varepsilon }^{Q}(\mathrm{u},{\mathrm{u}}^{\text{*}})\mathrm{C}{\varepsilon }^{L}({\mathrm{u}}_{1})\text{+}{\varepsilon }^{L}({\mathrm{u}}^{\text{*}})\mathrm{C}{\varepsilon }^{Q}(\mathrm{u},{\mathrm{u}}_{1})\text{+}{\varepsilon }^{Q}(\mathrm{u},{\mathrm{u}}^{\text{*}})\mathrm{C}{\varepsilon }^{Q}(\mathrm{u},{\mathrm{u}}_{1})\right]d\Omega \\ \text{=}0\end{array}\) eq 1.4.2-5 So the problem under consideration is unstable. |
We can express this bifurcation condition in matrix form by introducing, in addition, the geometric stiffness matrix \(K(\pi )\) which discretizes the first term:
\(\begin{array}{c}\forall {u}^{\text{*}}\mathrm{CA}\mathrm{0,}{u}^{\text{*}T}{K}_{t}{u}_{1}\text{=}0\\ \text{Avec}{K}_{T}\text{=}{K}_{0}\text{+}{K}^{L}(u)\text{+}{K}^{Q}(u)\text{+}K(\pi )\text{qui est la raideur tangente}\end{array}\) eq 1.4.2-6
If we write the bifurcation condition on the current configuration \({\Omega }_{S}\), then we have:
\(\forall {u}^{\text{*}}\text{CA}\mathrm{0,}{u}^{\text{*}T}[K\text{+}K(\sigma )]{u}_{1}\text{=}0\) eq 1.4.2-7
The constraint to be considered is then the Cauchy constraint and all the integrals are evaluated on the current domain \({\Omega }_{S}\).
1.4.2.1. Stability condition of a nonlinear elastic equilibrium#
It is immediately obvious that if there is a state such that the tangent matrix \({K}_{T}\) defined above is singular, we will have shown a non-zero displacement field \({u}_{1}\) which demonstrates the loss of uniqueness of the solution of the mechanical problem. This field of movement is the buckling mode. We can notice that the bifurcation condition is well verified, regardless of the norm and the sign of \({u}_{1}\): in this sense, we therefore speak of buckling mode, as a direction, because we limited ourselves in [éq 1.4.2-4] to the first order in \(\alpha\).
1.4.2.2. Case of short trips: Euler’s charge#
When the movements can be described as small before buckling, the initial configuration can be confused with the current geometry. The matrices \({K}^{L}\) and \({K}^{Q}\) can then be overlooked. In addition, the stress \(\pi\) can be confused with the usual stress \(\sigma\); the buckling equations are then written:
\([{K}_{0}\text{+}K(\sigma )]{u}_{1}\text{=}0\) eq 1.4.2.2-1
It should be noted that the matrix \(K(\sigma )\) is proportional to \(\sigma\) and therefore to the load applied to the structure. If we multiply the constraint by \(\lambda\), we get:
eq 1.4.2.2-2
This equation immediately brings to mind a generalized problem with eigenvalues, of the same type as in the case of the search for vibration modes, which is written:
\([{K}_{0}\text{-}{\omega }^{2}M]{v}_{1}\text{=}0\) eq 1.4.2.2-3
The matrix \(K(\sigma )\) is replaced by the mass matrix
, and we see the natural pulsation \(\omega\) appear, while \({v}_{1}\) is the associated vibration mode.
If one wishes to study buckling under a load where only a part of it is controlled (variable part of the load), by a principle of superposition, the constant contribution of the uncontrolled load must be added to the term \({K}_{0}\) and only the stress generated by the controlled load will be in the term in \(\lambda\). Formally, the following problem is therefore posed:
\([{K}_{0}\text{+}K({\sigma }_{\mathrm{cte}})\text{+}\lambda K({\sigma }_{\mathrm{var}})]{u}_{1}\)
\(\text{Avec :}\{\begin{array}{c}{\sigma }_{\mathrm{cte}}\text{: contrainte générée par le chargement non piloté}\\ {\sigma }_{\mathrm{var}}\text{: contrainte générée par le chargement piloté}\end{array}\) eq 1.4.2.2-4
The two constraint fields are obtained by solving two linear problems, one for the uncontrolled load, the other for the controlled part of the total load (cf. [U2.08.04] and [bib17]).
1.4.2.3. Special case of imposed forces depending on geometry#
Example of the following pressures:
When the external forces depend on the configuration, this means that the work of the external forces takes place in the condition of stability. Take the example of pressure applied to the structure. This pressure will be assumed to be constant during buckling: in other words, the pressure value does not change during movement.
This hypothesis corresponds to two types of real problems. The first type is that where the volume of the fluid imposing the pressure on the structure is very large compared to the volume variations generated by the displacement of the solid. The problems of tanks under internal pressure, where the displacements of the walls are not negligible compared to the dimensions of the structure itself, do not therefore fall within this framework.
The second case corresponds to the existence of a fluid source that makes it possible to maintain the pressure at a constant value. It is then no longer necessary to worry about the magnitude of the displacement of the solid.
Since the pressure value is taken to be fixed, the variation of the normal over time must be taken into account. This variation is due to the displacement field which changes the surface of the structure. Likewise, if we reason in terms of the resultant and therefore of the integral, the surface element can also change its area. Consequently, the resultant of the pressure forces will vary and this should be taken into account.
However, it is difficult to demonstrate the existence of potential. That is why we come back to the conservative case.
We quickly see that the power of the efforts, expressed on the current configuration, associated with pressure is given by the following equation (see for example [bib11]):
\({P}_{\text{pression}}^{\text{ext}}\text{=}\underset{\partial {\Omega }_{\mathrm{SP}}}{\int }p\left[n\text{+}\alpha \frac{{\mathrm{dS}}_{1}}{\mathrm{dS}}{n}_{1}\right]\text{.}{u}^{\text{*}}\mathrm{dS}\) eq 1.4.2.3-1
In this equation, we notice that the power of external forces is modified in displacement \(\alpha {u}_{1}\). We will then have:
\({P}_{1}^{\text{ext}}\text{=}{P}^{\text{ext}}\text{+}\underset{\partial {\Omega }_{\mathrm{SP}}}{\int }p\alpha {n}_{1}\text{.}{u}^{\text{*}}{\mathrm{dS}}_{1}\) eq 1.4.2.3-2
Finally, the matrix \({K}_{T}\) is enriched with an additional term, depending on the pressure:
\({K}_{T}\text{=}{K}_{0}\text{+}{K}^{L}(u)\text{+}{K}^{Q}(u)\text{+}K(\pi )\text{+}K(p)\) eq 1.4.2.3-3
If we write the operators on the current geometry, we end up with:
\({K}_{T}\text{=}K\text{+}K(\sigma )\text{+}K(p)\) eq 1.4.2.3-4
When we are in the presence of pressure-dependent forces, the same methods as those presented above can be applied to calculate buckling loads: it will suffice to complete matrix \({K}_{T}\) with the new term \(K(p)\). We can show that the \(K(p)\) matrix is symmetric if the pressure forces do not work on the « edge » of the model.
1.4.2.4. Vibrations under prestress#
The same methodology can also be applied to the study of structural vibrations in the current configuration \({\Omega }_{S}\). This structure is prestressed and deformed. All you have to do is write the geometric nonlinear Virtual Power Principle [éq 1.4.1-7] taking into account inertia effects and by injecting into it the hypothesis that displacements are periodic functions of the type:
\({\mathrm{u}}_{1}(t)\text{=}{\mathrm{v}}_{1}\text{sin}(\omega t)\) eq 1.4.2.4-1
From this it follows:
\(\mathrm{[}{\mathrm{K}}_{0}\text{+}{\mathrm{K}}^{L}(\mathrm{u})\text{+}{\mathrm{K}}^{Q}(\mathrm{u})\text{+}\mathrm{K}(\pi )\text{+}\mathrm{K}(p)\text{-}{\omega }^{2}\mathrm{M}\mathrm{]}{\mathrm{v}}_{1}\text{=}0\) eq 1.4.2.4-2
First of all, we notice, in this equation, that when we have a critical state then the natural vibration frequency of the structure corresponding to the buckling mode is zero.
In addition, we observe that the natural frequencies of the loaded structure are different from those of the initial structure for two reasons:
The natural pulsation \(\omega\) is modified by the prestress \(p\): this is the main effect that is used, for example, to tune a violin. The tension of the string affects the pitch of the corresponding note, and therefore on its natural frequency.
A second effect is the variation of the frequency by modification of the geometry: the initial geometric stiffness matrix
is replaced by the stiffness matrix on the current geometry: \({K}_{0}\text{+}{K}^{L}\text{+}{K}^{Q}\). This has the effect of modifying the vibratory equations.
The operator DYNA_NON_LINE allows vibration analyses to be carried out on the current non-linear configuration (keyword MODE_VIBR), but without taking into account prestress for the moment.
1.5. Implementation in the code#
With all rigor, in order to ensure the stability analysis of a non-linear quasistatic calculation, it is necessary to use the ad hoc stability criterion at each step of the incremental calculation. Any non-linear stability criterion must therefore be intrinsically as inexpensive as possible in terms of time CPU and in terms of memory.
Algorithmically speaking, it seems wise to implement the call to the criterion within the routine corresponding to the operator STAT_NON_LINE [bib15]. In fact, the principle of calling at each step is not well suited to a totally outsourced call to the incremental method of solving the non-linear mechanical problem.
1.6. Euler criterion#
This criterion (cf. [§1.4.2.2]) only requires the resolution of a linear static problem, then the construction and assembly of the geometric stiffness matrix. This and the assembled stiffness matrix are then to be passed as the argument of a solver [bib12] for the eigenvalue problem [éq 1.4.2.2-2].
At the output, the buckling modes and the corresponding critical loads are therefore recovered. For more details, the user can usefully consult the document [U2.08.04] [bib17].
1.7. Nonlinear criterion#
1.7.1. Impact on the operator STAT_NON_LINE#
Let’s start by briefly recalling how the incremental method for solving nonlinear structure problems works [bib15].
1.7.1.1. STAT_NON_LINE algorithm#
We will use the subscript*i* (like « instant ») to write down the number of a charge increment and the exponent n (like « Newton ») to note the number of the current Newton iteration. The algorithm used in operator STAT_NON_LINE can then be written schematically as follows:
\(({u}_{0},{\lambda }_{0})\) and \({\sigma }_{0}\) known
Loop over moments \({t}_{i}\) (or load increments): loading \({L}_{i}\text{=}L({t}_{i})\)
\(({u}_{i\text{-}1},{\lambda }_{i\text{-}1})\) known
Prediction: calculation of \(\Delta {u}_{i}^{0}\) and \(\Delta {\lambda }_{i}^{0}\)
Loop over Newton iterations: calculating a sequence \((\Delta {u}_{i}^{n},\Delta {\lambda }_{i}^{n})\)
\(({u}_{i}^{n},{\lambda }_{i}^{n})\) and \((\Delta {u}_{i}^{n},\Delta {\lambda }_{i}^{n})\) known
Calculation of matrices and vectors associated with follower loads
Expression of the behavioral relationship
calculation of the constraints \({\sigma }_{i}^{n}\) and the internal variables \({\alpha }_{i}^{n}\) using the values \({\sigma }_{l\text{-}1}\) and \({\alpha }_{l\text{-}1}\) at the previous equilibrium (\({t}_{i\text{-}1}\)) and the displacement increment \(\Delta {u}_{i}^{n}\text{=}{u}_{i}^{n}\text{-}{u}_{i\text{-}1}\) from this equilibrium
calculation of « nodal forces »: \({Q}^{T}{\sigma }_{i}^{n}\text{+}{B}^{T}{\lambda }_{i}^{n}\)
possible calculation of the tangent stiffness matrix: \({K}_{i}^{n}\text{=}K({u}_{i}^{n})\)
Calculation of the search direction \((\Delta {u}_{i}^{n\text{+}1},\Delta {\lambda }_{i}^{n\text{+}1})\) by solving a linear system
Linear search iterations: \(\rho\)
Updating variables and their increments:
\(\{\begin{array}{c}{u}_{i}^{n\text{+}1}\text{=}{u}_{i}^{n}\text{+}\rho \delta {u}_{i}^{n\text{+}1}\\ {\lambda }_{i}^{n\text{+}1}\text{=}{\lambda }_{i}^{n}\text{+}\rho \delta {\lambda }_{i}^{n\text{+}1}\end{array}\text{et}\{\begin{array}{c}{\Delta u}_{i}^{n\text{+}1}\text{=}\Delta {u}_{i}^{n}\text{+}\rho \delta {u}_{i}^{n\text{+}1}\\ \Delta {\lambda }_{i}^{n\text{+}1}\text{=}\Delta {\lambda }_{i}^{n}\text{+}\rho \delta {\lambda }_{i}^{n\text{+}1}\end{array}\)
Convergence test
Archiving the results at the moment \({t}_{i}\)
\(\{\begin{array}{c}{u}_{i}\text{=}{u}_{i\text{-}1}\text{+}\Delta {u}_{i}\\ {\lambda }_{i}\text{=}{\lambda }_{i\text{-}1}\text{+}\Delta {\lambda }_{i}\\ {\sigma }_{i}\\ {\alpha }_{i}\end{array}\)
Note that there are three levels of nested loops: an external loop over time steps, an iteration loop (qualified as global) Newton and possible sub-loops for linear research (if requested by the user) and certain behavioral relationships requiring iterations (so-called internal), for example for elasto-plasticity under plane constraints.
If we choose the criterion based on the assembled tangent matrix, we must have this matrix updated at each step where we want to do the stability analysis.
This is the case when a Newton method is used, and not a modified Newton method.
The following algorithm is then obtained:
\(({u}_{0},{\lambda }_{0})\) and \({\sigma }_{0}\) known
Loop over moments \({t}_{i}\) (or load increments): loading \({L}_{i}\text{=}L({t}_{i})\)
\(({u}_{i\text{-}1},{\lambda }_{i\text{-}1})\) known
Prediction: calculation of \(\Delta {u}_{i}^{0}\) and \(\Delta {\lambda }_{i}^{0}\)
Loop over Newton iterations: calculating a sequence \((\Delta {u}_{i}^{n},\Delta {\lambda }_{i}^{n})\)
\(({u}_{i}^{n},{\lambda }_{i}^{n})\) and \((\Delta {u}_{i}^{n},\Delta {\lambda }_{i}^{n})\) known
Calculation of matrices and vectors associated with follower loads
Expression of the behavioral relationship
calculation of the constraints \({\sigma }_{i}^{n}\) and the internal variables \({\alpha }_{i}^{n}\) using the values \({\sigma }_{l\text{-}1}\) and \({\alpha }_{l\text{-}1}\) at the previous equilibrium (\({t}_{i\text{-}1}\)) and the displacement increment \(\Delta {u}_{i}^{n}\text{=}{u}_{i}^{n}\text{-}{u}_{i\text{-}1}\) from this equilibrium
calculation of « nodal forces »: \({Q}^{T}{\sigma }_{i}^{n}\text{+}{B}^{T}{\lambda }_{i}^{n}\)
possible calculation of the tangent stiffness matrix: \({K}_{i}^{n}\text{=}K({u}_{i}^{n})\)
Calculation of the search direction \((\Delta {u}_{i}^{n\text{+}1},\Delta {\lambda }_{i}^{n\text{+}1})\) by solving a linear system
Linear search iterations: \(\rho\)
Updating variables and their increments:
\(\{\begin{array}{c}{u}_{i}^{n\text{+}1}\text{=}{u}_{i}^{n}\text{+}\rho \delta {u}_{i}^{n\text{+}1}\\ {\lambda }_{i}^{n\text{+}1}\text{=}{\lambda }_{i}^{n}\text{+}\rho \delta {\lambda }_{i}^{n\text{+}1}\end{array}\text{et}\{\begin{array}{c}{\Delta u}_{i}^{n\text{+}1}\text{=}\Delta {u}_{i}^{n}\text{+}\rho \delta {u}_{i}^{n\text{+}1}\\ \Delta {\lambda }_{i}^{n\text{+}1}\text{=}\Delta {\lambda }_{i}^{n}\text{+}\rho \delta {\lambda }_{i}^{n\text{+}1}\end{array}\)
Convergence test
Archiving the results at the moment \({t}_{i}\)
\(\{\begin{array}{c}{u}_{i}\text{=}{u}_{i\text{-}1}\text{+}\Delta {u}_{i}\\ {\lambda }_{i}\text{=}{\lambda }_{i\text{-}1}\text{+}\Delta {\lambda }_{i}\\ {\sigma }_{i}\\ {\alpha }_{i}\end{array}\)
Stability criterion, function of tangent stiffness updated: \({\mathrm{K}}_{i}^{n}\text{=}\mathrm{K}({\mathrm{u}}_{i}^{n})\)
The criterion is calculated at the end of the step, just after archiving. He therefore has as arguments the quantities converged at the current step. In addition, this choice of call position makes it possible to take account of follower loadings correctly, since their calculation is done during Newton iterations. The criterion cannot therefore be called before the end of these iterations.
1.7.1.2. Impact on the data structure result of STAT_NON_LINE#
Calling the nonlinear stability criterion will induce the resolution of an eigenvalue problem. The result of this calculation will therefore be a set of critical load/buckling mode pairs.
The critical loads are scalars and the associated modes are displacement fields, which will enrich the data structure resulting from STAT_NON_LINE.
1.7.3. Improving the performance of the criterion#
During the incremental resolution of a non-linear quasi-static problem, ideally and if we admit that the time discretization is sufficiently fine, a stability analysis should be carried out at each calculation step. At each step, this leads to the resolution of a problem with eigenvalues, which is certainly limited to the search for a few modes. Stability analysis therefore brings a significant additional cost CPU, to a non-linear calculation that can already be long.
The idea is to only use the resolution of an eigenvalue problem when it is really necessary, so when the current configuration is « close » to instability. If we can define this neighborhood by a predefined interval, then we can use a Sturm test [bib12].
This test makes it possible to know if there is at least one eigenvalue on the search interval. If yes, the modal search can then be carried out. Otherwise, the quasistatic incremental resolution is continued, without solving an eigenvalue problem.
The cost of a Sturm test is significantly lower than the cost of finding critical loads.
The search interval for the Sturm test can either be given by the user or have a default value in the code.
In the case of an updated Euler criterion (case of small deformations [§ 1.7.2.1]), where the problem to be solved is written as: \((\mathrm{K}\text{+}\lambda \mathrm{K}(\sigma ))\nu \text{=}0\) [éq 1.7.2.1-1], the search interval must be centered on the eigenvalue \(\lambda \text{=}1\) (which corresponds to the value -1 for the algorithm of CALC_MODES, because it actually solves a problem of the type: \(\mathrm{K}\nu \text{=}\mu \mathrm{K}(\sigma )\nu\))).
The limits of the interval are the limits of the multiplication factor of the load, and therefore of the dimensionless quantities, which are a function of the safety coefficients and the evaluation of the uncertainties for the given problem. The Sturm test is being implemented in this context.
In the specific case adapted to Green-Lagrange tensors [§ 1.7.2.2], where we solve: \((\mathrm{K}\text{+}\lambda \mathrm{I})\nu \text{=}0\) [éq 1.7.2.2-1], the interval is centered on 0. Moreover, the limits of the test interval are, contrary to the previous case, not dimensionless [§ 1.7.2.2]. It is therefore more difficult to identify relevant and general values (for the case of default values). The Sturm test is not currently implemented for this case.
1.8. Generalization to dynamics#
We will not discuss here the framework of dynamic instability criteria (negative amortization…). It’s just a matter of pointing out that the nonlinear criterion presented here can very well be applied directly in nonlinear dynamics. It will then detect any potential buckling of the structure, in the sense of the uniqueness of the updated global tangent stiffness matrix.
In order to be comprehensive in terms of stability analysis on a nonlinear dynamic study, the user should use two criteria:
a buckling criterion (stiffness criterion),
a dynamic criterion (criterion on damping or on the global quadratic linearized problem [bib14], for example).
For now, the buckling criterion on stiffness (identical to that of STAT_NON_LINE) is only available in DYNA_NON_LINE.
Coupled fluid-structure modeling (u, p, f) [R4.02.02] [], which is available in DYNA_NON_LINE, requires some adaptations in the use of the nonlinear stability criterion. In fact, this coupled formulation generates an intrinsically singular global stiffness matrix assembled on all fluid degrees of freedom, which makes it incompatible with the eigenvalue search method used for stability analysis. However, it is possible to get around the problem by correcting the assembled problem (stiffness and geometric stiffness matrix if necessary) using two specific keywords. The stability analysis then focuses on structural degrees of freedom alone.
1.9. Validation of developments#
The validation test cases are: SSNL126 and SSLL105D.
More specifically, test cases SSNL126 deal with the case of a beam embedded at one end and subjected to compression at the other end. The modeling is three-dimensional, with a relationship between elastoplastic behavior and linear isotropic work hardening. Two cinematic representations are presented:
modeling a: linearized deformations,
b modeling: Green-LaGrange deformations.
Test case SSLL105D is based on a beam problem in \(L\), whose elastic buckling is being studied. The finite elements are of the beam type.
1.10. Extension of the buckling criterion to the treatment of elastoplastic behavior#
Far from being exhaustive, we will present here only the simplest approaches, in order to easily implement them in the code.
When the structure operates in an elastoplastic regime, buckling is affected by the loss of strength due to plasticity [bib2]. The change comes from the behavior relationship during additional move \(\alpha {u}_{1}\).
In incremental form, the constraint becomes:
\(\Delta {\pi }_{1}\text{=}\Delta \pi \text{+}\alpha {C}_{T}[\Delta {\varepsilon }^{L}(u)\text{+}\Delta {\varepsilon }^{Q}(u,u)]\text{+}\frac{{\alpha }^{2}}{2}{C}_{T}\Delta {\varepsilon }^{Q}({u}_{1},{u}_{1})\) 1.11-1
In this expression, the behavior matrix is the tangent matrix \({C}_{T}\). The choice of this matrix is not immediate: in fact, the matrix depends on \(\alpha {\mathrm{u}}_{1}\) and is therefore not known as long as the mode is unknown. One can, for example, unload during buckling if the mode develops in one direction and charge if it develops in the opposite direction. It is therefore necessary to make a hypothesis for the behavior during plastic buckling. First, we will apply the Hill hypothesis [bib4] which assumes that the structure continues to charge plastically during buckling.
Let us consider an elastoplastic law of the Von Mises type. We define the three modules: \(E\) which is Young’s modulus, \({E}_{T}\) the tangent module, and the secant module. These modules are shown in the following figure:

|
Figure 1.11.5-a: Representation of the various modules on a 1D traction curve
Then we propose three possible methodologies.
The tangent module hypothesis simply consists in replacing Young’s modulus by the tangent modulus in the behavioral relationship. We then obtain:
\({C}_{T}\text{=}\frac{E}{{E}_{T}}C\) 1.11-2
This method is very rudimentary, but it is always pessimistic, which can be an advantage, if one looks at the dimensioning point of view.
The method usually used consists in using the tangent matrix of the incremental calculation (operator STAT_NON_LINE [bib15]). So we have the following equation in the case of Von Mises plasticity [bib16]:
\({C}_{T}\text{=}C\left[I\text{-}\frac{A[{\sigma }^{D}\otimes {\sigma }^{{D}^{T}}]AC}{h\text{+}\frac{{\sigma }^{{D}^{T}}AA{\sigma }^{D}}{{\parallel {\sigma }^{D}\parallel }_{\mathrm{VM}}}}\right]\)
\(\text{Avec}\{\begin{array}{c}{\sigma }^{D}\text{: vecteur déviateur des contraintes}\\ A\text{: matrice intervenant dans la norme de VonMises}({\parallel {\sigma }^{D}\parallel }_{\mathrm{VM}}\text{=}\sqrt{{\sigma }^{{D}^{T}}A{\sigma }^{D}})\\ h\text{:pente plastique définie par}h\text{=}\frac{E\text{.}{E}^{T}}{E\text{-}{E}^{T}}\end{array}\) 1.11-3
This method is only perfectly rigorous in terms of non-linear elasticity or if we respect the Hill hypothesis: it does not make it possible to predict bifurcations in loading paths. As soon as the behavioral relationship is dissipative (see chapter 2), the calculated critical loads will only be accurate if it can be verified that the load is monotonic, at any point in the structure (Hill [bib4]).
The most realistic method is to use the finite deformation theory only to calculate the plastic buckling load. The tangent behavior matrix is given by the equation below:
\({C}_{T}\text{=}{\left[(\frac{1}{{E}_{T}}\text{-}\frac{1}{{E}_{S}})\frac{A[{\sigma }^{D}\otimes {\sigma }^{{D}^{T}}]A}{{\parallel {\sigma }^{D}\parallel }_{\mathrm{VM}}}\text{+}{C}^{\text{-}1}\text{+}(\frac{1}{{E}_{S}}\text{-}\frac{1}{E})A\right]}^{\text{-}1}\) 1.11-4
Compared to the method based on the tangent stiffness matrix [éq 1.11-3], this criterion requires the construction and assembly of a specific global matrix. This costly operation increases the incremental resolution.
For reasons of generality and to minimize the development cost and the calculation cost (CPU and memory), we therefore choose the criterion based on the tangent module [éq 1.11-3].
1.11. Conclusion#
Code_Aster offers two stability criteria, in the sense of buckling, for structural calculations:
On the one hand, in cases where a linearized approach is sufficient, it is possible to apply an Euler-type criterion ([bib13] and [bib18]), by calling on a generalized eigenvalue problem solving operator (CALC_MODES with the keyword TYPE_RESU =” MODE_FLAMB “).
On the other hand, for all cases where it is essential to take into account non-linearities, whether they are due to the behavioral relationship or to large transformations, the user can use a suitable criterion, of the generalized Euler type. This criterion is called during the incremental resolution of the quasi-static problem (operator STAT_NON_LINE).
[bib15]).
At each time step, the criterion is based on solving a problem with eigenvalues [bib13] on the updated global stiffness matrices. This criterion, which comes in two different forms, depending on the deformation tensor chosen, is based on a linearization around the current calculation step. It accepts any type of deformation tensor, as well as any type of behavioral relationship for which one is able to build the global stiffness matrix, at any moment. Moreover, the criterion chosen is perfectly rigorous in the case of nonlinear elastic behavior relationships, and can be extended to the case of elastoplasticity associated with the Hill hypothesis [bib4].