3. Digital integration#
3.1. Unknowns and equations of the nonlinear system#
The model is integrated implicitly (@ DSL Implicit) via the Mfront tool. The « numerical » internal variables make up the vector
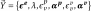
. In the case where both mechanisms are active, i.e.
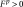
and

at the end of the elastic prediction phase (@Predictor), the equations constitutive of the non-linear system to be solved at the moment
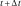
during the correction phase are,
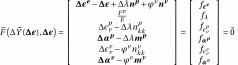
(3.1)
The non-linear system is also solved in the case where only one of the two mechanisms is activated at the end of the prediction phase, i.e.

or

. In the rest of the document, we will detail only the terms deriving from the system (); the particular cases for which

and
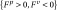
can be easily deduced from () by taking some null terms.
Note: if the user takes
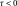
, the viscoplastic mechanism is deactivated.
3.2. Flow directions#
The flow directions associated with

,
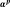
,

, and

are respectively given by,

(3.2)
with,
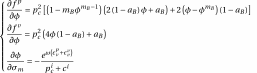
(3.3)
3.3. Tangent operator#
3.3.1. Tangent operator expression#
The stress tensor

unto
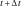
is assumed to be a function of
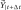
and
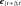
,
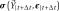
(3.4)
The coherent tangent operator is given by,

(3.5)
Furthermore, through differentiation,
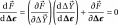
(3.6)
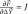
is the Jacobian matrix of the nonlinear system to be solved. Finally, the tangent operator is expressed,
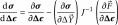
(3.7)
Equation () can be simplified in the particular case where, 1 —
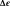
only appears in
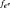
(deformation tensor partition), and 2 —

only depends on
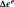
via Hooke’s law. In this case,
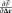
takes the following form,

(3.8)
And the product
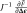
only involves the first six columns of
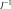
; sub-matrix that we note
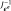
. Furthermore, Hooke’s law gives,

(3.9)
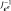
is obtained from

using function MFrontgetPartialJacobianInvert.
3.3.2. Expression of the Jacobian matrix of the system#
The Jacobian matrix of the system

,

, is given by,

(3.10)
In MFront, this matrix can be obtained by numerical disturbance — @Algorithm NewtonRaphson_NumericalJacobian — or analytically, as is the case here. The components of

are detailed below in case both mechanisms are activated.
3.3.2.1. First line of the Jacobienne#
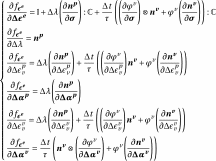
(3.11)
Expressions for derivatives of
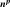
are,
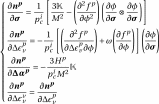
(3.12)
with,
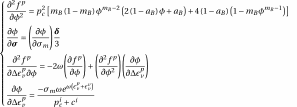
(3.13)
Expressions for derivatives of

are,
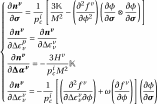
(3.14)
with,
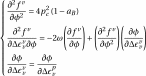
(3.15)
Expressions for derivatives of

are,
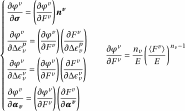
(3.16)
with,
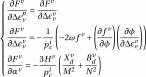
(3.17)
3.3.2.2. Second line of the Jacobian#
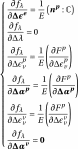
(3.18)
Expressions for derivatives of
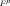
are,
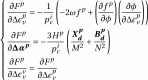
(3.19)
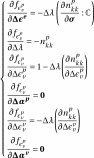
3.3.2.3. Third line of the Jacobian#
(3.20)
Expressions for derivatives of
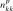
are,
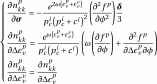
(3.21)
3.3.2.4. Fourth line of the Jacobian#
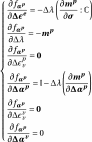
(3.22)
Expressions for derivatives of
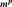
are,
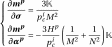
(3.23)
3.3.2.5. Fifth line of the Jacobian#

(3.24)
Expressions for derivatives of
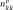
are,
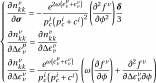
(3.25)
3.3.2.6. Sixth line of the Jacobian#

(3.26)
Expressions of derivatives of
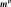
are,
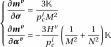
(3.27)