2. Constitutive equations#
2.1. Free energy#
Free energy is in the following general form,
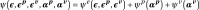
(2.1)
with,
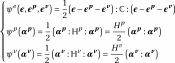
(2.2)

is the strain tensor,

is the tensor of plastic deformations,

is the tensor of viscoplastic deformations,
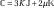
is the Hooke tensor —

and

are respectively the compressibility and shear modules,

and

are respectively the spherical and deviatoric projectors —
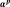
and
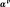
are state variables associated respectively with plastic and viscoplastic mechanisms,
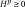
and

are homogeneous to work hardening modules [Pa]; these are material parameters of the model.
2.2. Thermodynamic forces#
Thermodynamic forces associated with state variables

,

,

,
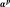
, and
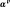
are respectively,
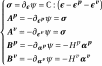
(2.3)
2.3. Plasticity and viscoplasticity criteria#
The evolution of the maximum strength of cohesive geomaterials as a function of the average stress,
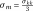
, is generally non-linear. The plasticity criteria most used in rock mechanics are commonly inspired by the work of Hoek & Brown,
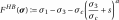
(2.4)
where
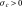
[Pa] represents the resistance to simple compression,
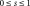
[-] is a « cohesion » parameter, and
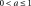
[-] is a parameter linked to the « dilating » nature of the material.
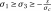
are the main major and minor constraints respectively.
The criteria used in models LETK and LKR constitute generalizations — written according to the invariants of the stress tensor and its deviator — of the Hoek-Brown criterion.
The main disadvantage of these « parabolic » criteria is that they do not close to the hydrostatic axis. The application of the law of normality of plastic flow therefore produces only dilating volume plastic deformations for any average stress.

. Therefore, geomechanics often use so-called « non-associated » formulations; which make it possible to better represent the contract/dilatance transition (characteristic state) and the critical state, (
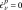
to the « large deformations ») observed in most geomaterials.
Recourse to non-associativity does not make it possible — a priori — not to ensure compliance with the framework of generalized standard materials, which generally guarantees good numerical convergence properties of laws of behavior.
The form of criterion selected — as part of this modernization process — is based on the work of. The criterion proposed by can be considered as an evolution of the Cam-Clay elliptic criterion, which makes it possible to distort the initial ellipse into more or less deformed ovoid. The general expression of the plasticity and viscoplasticity criteria is given by,
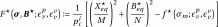
(2.5)
with
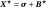
,
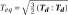
,

,
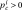
[Pa] is assimilated to a pre-consolidation stress (in the sense of Cam-Clay) in isotropic compression (intersection of
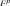
with the hydrostatic axis on the compression side),
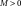
[-] is the original critical state slope of the Cam-Clay criterion,
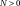
[-] is a material parameter involved in the expression of a new critical state slope (translated by kinematic work hardening),

is a function of the average stress state, which takes different mathematical forms for plastic and viscoplastic surfaces,
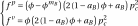
(2.6)
with,
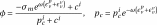
(2.7)
The shapes chosen for

and

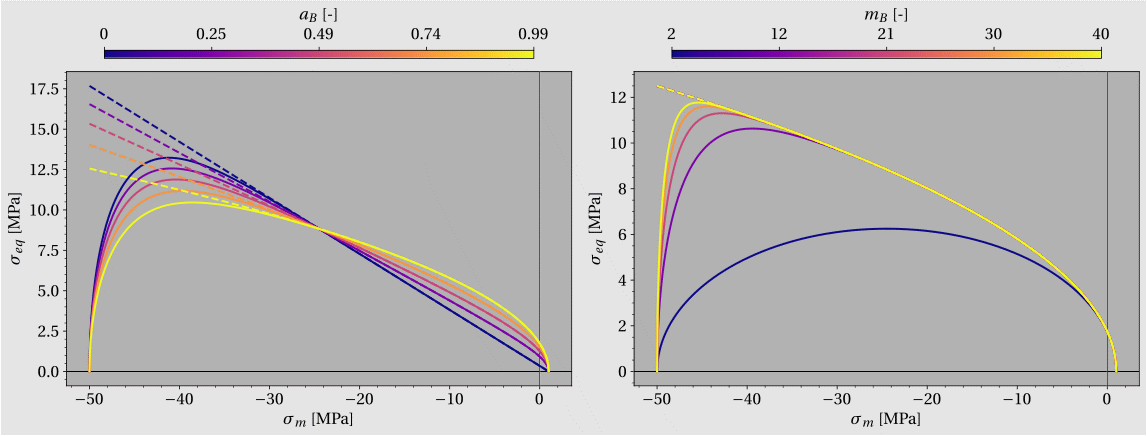
lead respectively to closed and open plasticity and viscoplasticity criteria (Fig.). This choice is motivated by the desire to be able to — 1. reproduce the fragile/ductile and dilatance/contraction transitions under « instantaneous » triaxial compression, i.e. reproduce the dependence of plastic behavior on the average stress state — 2. to avoid any delayed behavior when the stress state is purely hydrostatic, i.e. no spherical creep; which is very little observed for cohesive materials at low porosity.
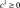
[Pa] is assimilated to an elastic limit under tension,
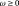
[-] controls the « scalar » work hardening kinetics,
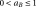
[-] and

[-] are the so-called « Bigoni » parameters, which make it possible to distort the original Cam-Clay ellipse (Fig.).
In the rest of the document, the sign convention adopted is that of Mechanics of Continuous Environments, i.e. negative compressions, positive tractions.
Figure 1: Initial elasticity limits of plastic (solid lines) and viscoplastic (dashes) mechanisms for various parameter values
and

2.4. Plastic and viscoplastic flows#
The increments of the state variables are given by the law of normality,
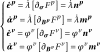
(2.8)
where

is the plastic multiplier — whose increment is obtained by applying Kuhn-Tucker compatibility conditions — and

is a viscosity coefficient, whose expression is inspired by the work of Perzyna,
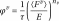
(2.9)

[s] is a characteristic time,
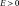
[Pa] is Young’s modulus,
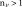
[-] is a parameter that controls the kinetics of delayed phenomena.