3. Model description#
3.1. Clean creep#
3.1.1. Description of the spherical part of the natural creep#
Spherical stresses are at the origin of the migration of water adsorbed at the interfaces between hydrates at the macro-porosity level and absorbed within the micro-porosity in the capillary porosity. The diffusion of inter-lamellar water from the hydrate pores to the capillary porosity takes place irreversibly. The total spherical creep deformation is therefore written as the sum of a reversible part and an irreversible part:
\({\epsilon }^{\text{fs}}=\underset{\begin{array}{}\text{partie}\\ \text{réversible}\end{array}}{\underset{\underbrace{}}{{\epsilon }_{r}^{\text{fs}}}}+\underset{\begin{array}{}\text{partie}\\ \text{irréversible}\end{array}}{\underset{\underbrace{}}{{\epsilon }_{i}^{\text{fs}}}}\) eq 3.1.1-1
The process of spherical creep deformation is governed by the following system of coupled equations (equations [éq 3.1.1-2] and [éq 3.1.1-3]):
\({\dot{\epsilon }}^{\text{fs}}=\frac{1}{{\eta }_{r}^{s}}\cdot \left[h\cdot {\sigma }^{s}-{k}_{r}^{s}\cdot {\epsilon }_{r}^{\text{fs}}\right]-{\dot{\epsilon }}_{i}^{\text{fs}}\) eq 3.1.1-2
where \({k}_{r}^{s}\) refers to the apparent stiffness associated with the skeleton formed by hydrate blocks at the mesoscopic scale;
and \({\eta }_{r}^{s}\) the apparent viscosity associated with the diffusion mechanism within the capillary porosity.
\({\dot{\epsilon }}_{i}^{\text{fs}}=\frac{1}{{\eta }_{i}^{s}}{\langle \left[{k}_{r}^{s}\cdot {\epsilon }^{\text{fs}}-({k}_{r}^{s}+{k}_{i}^{s})\cdot {\epsilon }_{i}^{\text{fs}}\right]-\left[{\mathrm{h\sigma }}^{s}-{k}_{r}^{s}\cdot {\epsilon }_{r}^{\text{fs}}\right]\rangle }^{+}\) eq 3.1.1-3
where \({k}_{i}^{s}\) refers to the apparent stiffness intrinsically associated with hydrates at the microscopic scale;
and \({\eta }_{i}^{s}\) the apparent viscosity associated with the mechanism of inter-foliar diffusion.
In [éq 3.1.1-3], the \({\langle \rangle }^{+}\) brackets refer to the Mac Cauley operator: \({\langle x\rangle }^{+}=\frac{1}{2}(x+\mid x\mid )\)
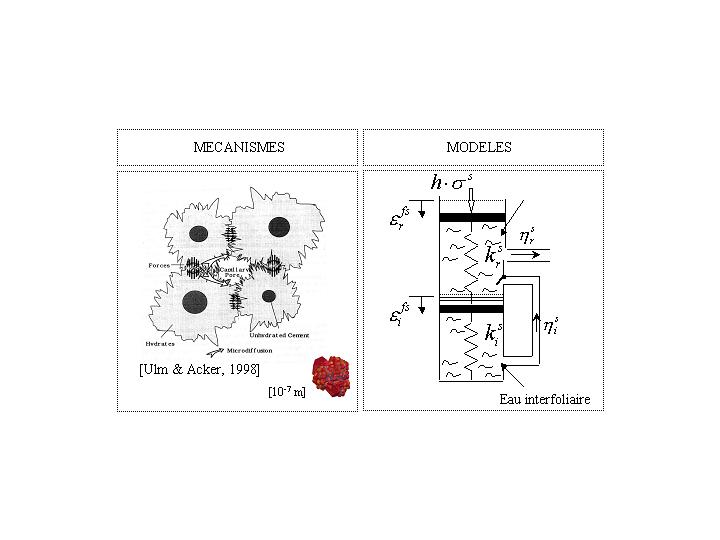
Figure 3.1.1-1:Phenomenological model associated with the spherical part of natural creep
3.1.2. Description of the deviatoric part#
Deviatory stresses are at the origin of a sliding mechanism (or mechanism of virtual dislocation) of sheets of CSH in nano-porosity. Under deviatoric stress, creep takes place at constant volume. Moreover, creep law UMLV assumes the isotropy of deviatoric creep. Phenomenologically, the sliding mechanism includes a reversible viscoelastic contribution of water strongly adsorbed to the sheets of CSH and an irreversible viscous contribution of free water:
\(\underset{\begin{array}{}\text{déformation}\\ \text{déviatorique}\\ \text{totale}\end{array}}{\underset{\underbrace{}}{{\underline{\underline{\epsilon }}}^{\text{fd}}}}=\underset{\begin{array}{}\text{contribution}\\ \text{eau}\\ \text{absobée}\end{array}}{\underset{\underbrace{}}{{\underline{\underline{\epsilon }}}_{r}^{\text{fd}}}}+\underset{\begin{array}{}\text{contribution}\\ \text{eau}\\ \text{libre}\end{array}}{\underset{\underbrace{}}{{\underline{\underline{\epsilon }}}_{i}^{\text{fd}}}}\) eq 3.1.2-1
The*th* main component of total deviatoric deformation is governed by equations [éq. 3.1.2-2] and [éq 3.1.2-3]:
\({\eta }_{r}^{d}{\dot{\epsilon }}_{r}^{d,j}+{k}_{r}^{d}{\epsilon }_{r}^{d,j}=h\cdot {\sigma }^{d,j}\) eq 3.1.2-2
\({\eta }_{i}^{d}{\dot{\epsilon }}_{i}^{d,j}=h\cdot {\sigma }^{d,j}\) eq 3.1.2-3
where \({k}_{r}^{d}\) refers to the stiffness associated with the capacity of adsorbed water to transmit loads (load bearing water), \({\eta }_{r}^{d}\) the viscosity associated with the water adsorbed by the hydrate sheets and \({\eta }_{i}^{d}\) refers to the viscosity of free water.
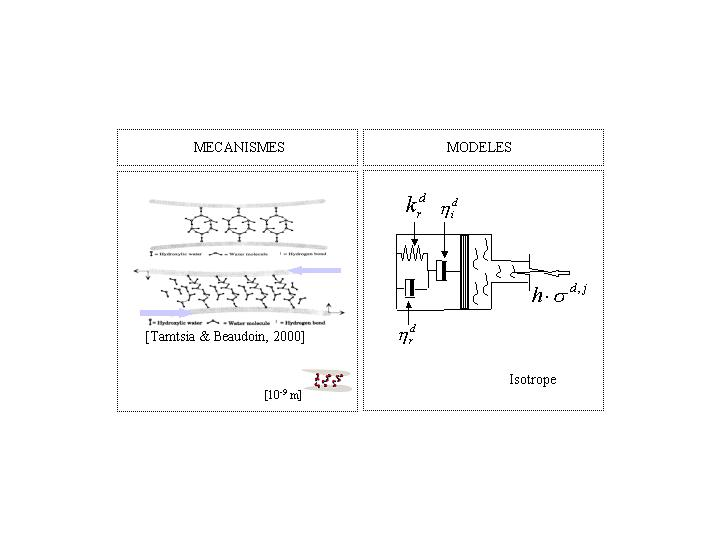
Figure 3.1.2-1: Phenomenological model associated with the deviatoric part of natural creep.
3.2. Desiccation creep#
It is assumed to be able to break down desiccation creep \({\mathit{\Delta \epsilon }}^{\mathit{fdess}}\) into two parts called intrinsic and structural [bib4]:
\({\mathit{\Delta \epsilon }}^{\mathit{fdess}}={\mathit{\Delta \epsilon }}_{\text{int}}^{\text{fdess}}+{\mathit{\Delta \epsilon }}_{\text{struct}}^{\text{fdess}}\) eq 3.2-1
It is agreed that structural deformation is not a deformation component in itself, so in this document the only component of desiccation creep concerns the intrinsic part:
\({\mathit{\Delta \epsilon }}^{\text{fdess}}={\mathit{\Delta \epsilon }}_{\text{int}}^{\text{fdess}}\) eq 3.2-2
Bazant et al. [bib10] suggest that drying and applying a compression load simultaneously are responsible for the microdiffusion of molecules between macro-pores and micro-pores. The micro-diffusion of water molecules would promote the breaking of the bonds between the gel particles inducing the deformation of desiccation creep. It is one of the most complicated physicochemical phenomena to model resulting from a coupling between stress, natural creep and drying. They propose the following equation (shock absorber equation) to take into account the (intrinsic) desiccation creep at the elementary level:
- math:
{dot {epsilon}}} ^ {text {fdess}} =frac {left|dot {h}right|sigma} {{mathrm {eta}}} ^ {mathrm {eta}}} ^ {mathit {fdess}}} eq 3.2-3
with:
\({\epsilon }^{\text{fdess}},\) the deformation of the desiccation creep,
\({\eta }^{\mathit{fd}}\) a material parameter (in \(\left[\mathit{Pa}\cdot \mathit{sec}\right]\) in the S.I.),
\(h,\) the relative humidity that changes over time, given the evolution problem.