4. Rotation vector and operator

Appendix 1 gives preliminary results concerning antisymmetric matrices of order 3.

4.1. Vector-rotation

Suppose that, in the system of general axes \(P\text{}{e}_{1}\text{}{e}_{2}\text{}{e}_{3}\) [fig 4.1-a], the point \(M\text{'}\) is deduced from \(M\) by the rotation of angle \(\alpha\) around the axis passing through \(P\) and by the unit vector \(u\). Let’s say:

\(\Psi =\alpha u\)

\(\Psi\) is called the rotation-vector to go from \(M\) to \(M\text{'}\).

According to the Euler-Rodrigues formula [bib6] p. 186 and [bib7]:

\(\overrightarrow{\mathrm{PM}\text{'}}=\overrightarrow{\mathrm{PM}}+\text{sin}\alpha (u\wedge \overrightarrow{\mathrm{PM}})+(1-\mathrm{cos}\alpha )\left[u\wedge \left[u\wedge \overrightarrow{\mathrm{PM}}\right]\right]\).

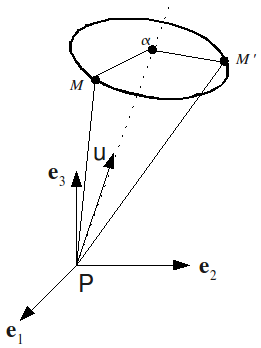
Figure 4.1-a: Representation of a finite rotation

In general, the rotation vector of the product of two rotations isn’t the geometric sum of the component rotation vectors. The 2D case is a particularly simple exception: the vectors-rotation, perpendicular to the plane, are added algebraically.

4.2. Rotation operator

Given [éq An1-3], the previous equation is written as:

\(\overrightarrow{\mathrm{PM}\text{'}}=\left[1+\mathrm{sin}\alpha \stackrel{ˆ}{u}+(1-\mathrm{cos}\alpha ){\stackrel{ˆ}{u}}^{2}\right]\overrightarrow{\mathrm{PM}}\)

The expression in square brackets defines the rotation operator \(R\) to go from \(\mathrm{PM}\) to \(\mathrm{PM}\text{'}\):

\(R=1+\text{sin}\alpha \stackrel{ˆ}{u}+(1-\text{cos}\alpha ){\stackrel{ˆ}{u}}^{2}\text{.}\) eq 4.2-1

The following four numbers are called « Euler parameters » of rotation:

\(\begin{array}{cc}{e}_{0}=\text{cos}\frac{\alpha }{2}& {e}_{1}=\text{sin}\frac{\alpha }{2}{u}_{1}\\ {e}_{2}=\text{sin}\frac{\alpha }{2}{u}_{2}& {e}_{3}=\text{sin}\frac{\alpha }{2}{u}_{3}\end{array}\) eq 4.2-2

Of course we have:

\({e}_{0}^{2}+{e}_{1}^{2}+{e}_{2}^{2}+{e}_{3}^{2}=1\text{.}\)

Let’s say:

\(e=\left\{\begin{array}{c}{e}_{1}\\ {e}_{2}\\ {e}_{3}\end{array}\right\}=\text{sin}\frac{\alpha }{2}u\text{.}\)

Using the [éq A1-4] relationship, you can easily put the expression [éq 4.2-1] for \(R\) in the form:

\(R=(2{e}_{0}^{2}-1)1+2({ee}^{T}+{e}_{0}\stackrel{ˆ}{e})\text{.}\) eq 4.2-3

On the other hand, replacing \(\text{sin}\alpha\) and \(\text{cos}\alpha\), to the second member of [éq 4.2-1], by their developments in entire series, he comes:

\(\begin{array}{cc}R=1& +\left[\alpha -\frac{{\alpha }^{3}}{3!}+\frac{{\alpha }^{5}}{5!}+\text{...}+{(-1)}^{p-1}\frac{{\alpha }^{\mathrm{2p}-1}}{(\mathrm{2p}-1)!}+\text{...}\right]\stackrel{ˆ}{u}\\ & +\left[\frac{{\alpha }^{2}}{2!}-\frac{{\alpha }^{4}}{4!}+\frac{{\alpha }^{6}}{6!}+\text{...}+{(-1)}^{p-1}\frac{{\alpha }^{\mathrm{2p}}}{(\mathrm{2p})!}\right]{\stackrel{ˆ}{u}}^{2}\end{array}\)

or, using [éq A1-5] and [éq A1-6], the exponential form of the rotation operator:

\(\begin{array}{c}R=1+\alpha \stackrel{ˆ}{u}+\frac{{(\alpha \stackrel{ˆ}{u})}^{2}}{2!}+\text{...}+\frac{{(\alpha \stackrel{ˆ}{u})}^{p}}{p!}+\text{...}\\ =\text{exp}(\alpha \stackrel{ˆ}{u})=\text{exp}(\stackrel{ˆ}{\Psi })\text{.}\end{array}\) eq 4.2-4

It appears on [éq 4.2-4] that when \(\parallel \Psi \parallel \to 0\),

\(R\approx 1+\Psi \wedge \text{.}\) eq 4.2-5

\(R=\text{exp}(\alpha \stackrel{ˆ}{u})\) is obviously not calculated by the development [éq 4.2-4], but by the expression [éq 4.2-1].

Since \({\stackrel{ˆ}{u}}^{T}=-\stackrel{ˆ}{u}\), transposing all the terms on the second member of [éq 4.2-4] gives:

\({\left[\text{exp}(\stackrel{ˆ}{\Psi })\right]}^{T}=\text{exp}(-\stackrel{ˆ}{\Psi })\), i.e.: eq 4.2-6

\({R}^{T}={R}^{-1}\)

and:

\({\mathrm{RR}}^{T}=1\) eq 4.2-7

The rotation operators, orthogonal according to the equation [éq 4.2-7], form a group in relation to the multiplication operation - non-commutative in 3D - called Lie group and designated by \(\text{SO}(3)\) (Special Orthogonal group).