8. MAZARS model in 1D#

8.1. Model equations#

The objective of this modeling is to account for the closure of cracks. This model is only used with multi-fiber beams. The equations presented in the document [R7.01.08] « Mazars damage model » are taken over and rewritten in \(\mathrm{1D.}\)

\(\mathrm{\{}\begin{array}{c}{\sigma }_{\mathit{xx}}\mathrm{=}(1\mathrm{-}{D}_{t})E{\mathrm{\langle }{\varepsilon }_{\mathit{xx}}^{e}\mathrm{\rangle }}_{\text{+}}\\ {\sigma }_{\mathit{xx}}\mathrm{=}(1\mathrm{-}{D}_{c})E{\mathrm{\langle }{\varepsilon }_{\mathit{xx}}^{e}\mathrm{\rangle }}_{\text{-}}\end{array}\)

with:

  • \(E\): Young’s module,

  • \({D}_{t}\): the damage variable under traction.

  • \({D}_{c}\): the compression damage variable.

  • \({\varepsilon }_{\mathit{xx}}^{e}\): elastic deformation \({\varepsilon }_{\mathit{xx}}^{e}\mathrm{=}\varepsilon \mathrm{-}{\varepsilon }^{\mathit{th}}\)

• \({\varepsilon }^{\mathit{th}}\mathrm{=}\alpha (T\mathrm{-}{T}_{\mathit{ref}})\) : thermal expansion

The damage is always controlled by the extensions.

Tensile damage exists if \({\mathrm{\epsilon }}_{\mathit{eq}}\ge {\mathrm{\epsilon }}_{t0}\), compression damage exists if \({\mathrm{\epsilon }}_{\mathit{eq}}\ge {\mathrm{\epsilon }}_{c0}\):

\({D}_{c}=1-\frac{{\mathrm{\epsilon }}_{c0}\left(1-{A}_{c}\right)}{{\mathrm{\epsilon }}_{\mathit{eq}}}-\frac{{A}_{c}}{\text{exp}\left[{B}_{c}({\mathrm{\epsilon }}_{\mathit{eq}}-{\mathrm{\epsilon }}_{c0})\right]}\phantom{\rule{6em}{0ex}}{D}_{c}\in \text{[}0,1\text{[}\)

\({D}_{t}=1-\frac{{\mathrm{\epsilon }}_{t0}\left(1-{A}_{t}\right)}{{\mathrm{\epsilon }}_{\mathit{eq}}}-\frac{{A}_{t}}{\text{exp}\left[{B}_{t}({\mathrm{\epsilon }}_{\mathit{eq}}-{\mathrm{\epsilon }}_{t0})\right]}\phantom{\rule{6em}{0ex}}{D}_{t}\in \text{[}0,1\text{[}\)

where \({A}_{c},{A}_{t},{B}_{c},{B}_{t},{\mathrm{\epsilon }}_{c0},{\mathrm{\epsilon }}_{t0}\) are material parameters to be identified.

The damage is driven by the equivalent deformation \({\varepsilon }_{\mathit{eq}}\). Extensions are essential in the phenomenon of concrete cracking. The equivalent deformation introduced is defined from the positive values of the deformations, i.e.:

math:

{begin {array} {c} {c}text {Si} {epsilon} _ {mathit {xx}}} ^ {e}ge 0text {epsilon} {epsilon} _ {epsilon} _ {mathit {eq}}} =| {mathit {eq}}} =| {epsilon} _ {mathit {xx}} ^ {e} |\ text {epsilon} _ {\ text {epsilon} _ {epsilon}} |\text {Si} {epsilon} _ {epsilon}} |\text {Si} {epsilon}} on} _ {mathit {xx}} ^ {e}} ^ {e}le 0text {then} {epsilon} _ {mathit {eq}} =sqrt {2}nu | {epsilon}} _ {epsilon} _ {epsilon} _ {epsilon} _ {epsilon} _ {mathit {xx}}} ^ {e} |end {array}

Note:

In the case where \({\varepsilon }_{\mathit{xx}}^{e}\mathrm{\le }0\), in \(\mathrm{1D}\) the main deformations in the other directions are \({\varepsilon }_{\mathit{yy}}^{e}\mathrm{=}{\varepsilon }_{\mathit{zz}}^{e}\mathrm{=}\mathrm{-}\nu {\varepsilon }_{\mathit{xx}}^{e}\). By using the formula \({\varepsilon }_{\text{eq}}\mathrm{=}\sqrt{{\mathrm{\langle }{\varepsilon }_{1}\mathrm{\rangle }}_{\text{+}}^{2}+{\mathrm{\langle }{\varepsilon }_{2}\mathrm{\rangle }}_{\text{+}}^{2}+{\mathrm{\langle }{\varepsilon }_{3}\mathrm{\rangle }}_{\text{+}}^{2}}\) we get the previous expression.

The tangent matrix has for expression: \(\frac{d{\sigma }_{\mathit{xx}}}{d{\varepsilon }_{\mathit{xx}}^{e}}\mathrm{=}(1\mathrm{-}\tilde{D})E\mathrm{-}\frac{d\tilde{D}}{d{\varepsilon }_{\mathit{xx}}^{e}}E{\varepsilon }_{\mathit{xx}}^{e}\) with:

\(\begin{array}{ccc}\text{Si}{\mathrm{\epsilon }}_{\mathit{xx}}^{e}\ge 0\text{et}{\mathrm{\epsilon }}_{\mathit{eq}}\ge {\mathrm{\epsilon }}_{t0}& \frac{d\stackrel{~}{D}}{d{\mathrm{\epsilon }}_{\mathit{xx}}^{e}}\text{=}\frac{d{D}_{t}}{d{\mathrm{\epsilon }}_{\mathit{xx}}^{e}}\text{=}& \left(\frac{{\mathrm{\epsilon }}_{t0}\left(1-{A}_{t}\right)}{{\mathrm{\epsilon }}_{\mathit{eq}}^{2}}+\frac{{A}_{t}{B}_{t}}{\mathrm{exp}\left[{B}_{t}({\mathrm{\epsilon }}_{\mathit{eq}}-{\mathrm{\epsilon }}_{t0})\right]}\right)\\ \text{Si}{\mathrm{\epsilon }}_{\mathit{xx}}^{e}<0\text{et}{\mathrm{\epsilon }}_{\mathit{eq}}\ge {\mathrm{\epsilon }}_{c0}& \frac{d\stackrel{~}{D}}{d{\mathrm{\epsilon }}_{\mathit{xx}}^{e}}\text{=}\frac{d{D}_{c}}{d{\mathrm{\epsilon }}_{\mathit{xx}}^{e}}\text{=}& -\sqrt{2}\mathrm{\nu }\left(\frac{{\mathrm{\epsilon }}_{c0}\left(1-{A}_{c}\right)}{{\mathrm{\epsilon }}_{\mathit{eq}}^{2}}+\frac{{A}_{c}{B}_{c}}{\mathrm{exp}\left[{B}_{c}({\mathrm{\epsilon }}_{\mathit{eq}}-{\mathrm{\epsilon }}_{c0})\right]}\right)\end{array}\)

The test cases [V6.02.120], [V6.02.119], [V5.02.130] implement the Mazars law of behavior in version \(\mathrm{1D}\).

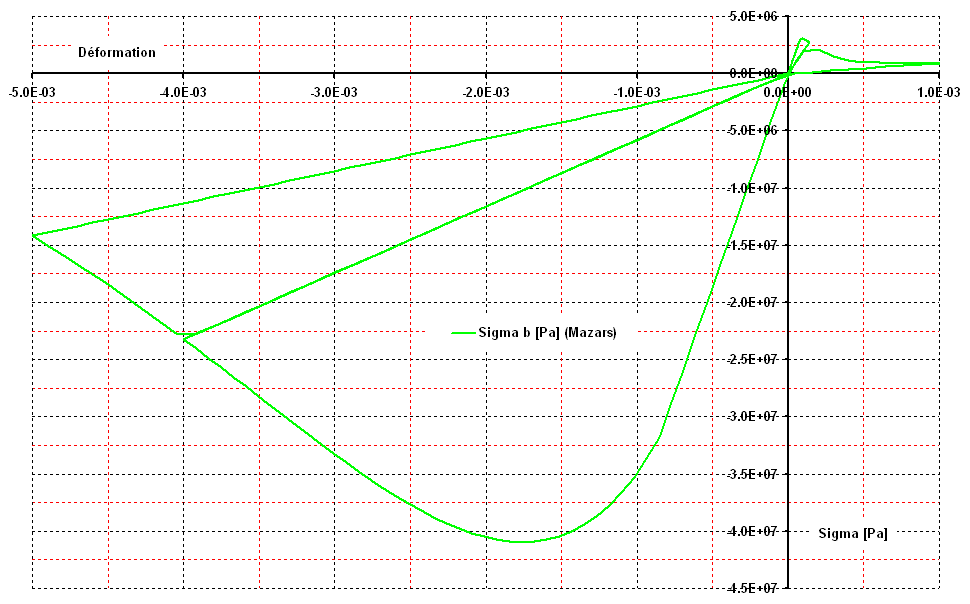
_images/10000200000003CA0000025C27D4D79DB8030995.png

Figure 8.1-a: Mazars behavior in version \(\mathrm{1D}\).

8.2. Internal variables#

The law of behavior is written by decoupling tensile and compression damages, the two damages are no longer internal variables [R7.01.08].

This law is dedicated to civil building structure calculations. To facilitate the interpretation of the results, two variables are created to describe the « limit » state of the concrete material, in accordance with what is done in the regulations for the design of reinforced concrete at limit states.

  • The variable CRITSIG gives information about the stress state. This variable represents the stress divided by the concrete limit stress given by user SIGM_LIM.

  • Variable CRITEPS gives information about the state of deformation. This variable represents the equivalent deformation \({\varepsilon }_{\mathit{eq}}\) divided by the limiting deformation given by the user using the EPSI_LIM keyword.

The values of the limiting stress SIGM_LIM and the limiting deformation EPSI_LIM can be modified by the user when defining the material: defi_materiau [U4.43.01], DEFI_MATE r_GC [U4.42.07].

Writing Mazars’s law does not make it possible to calculate a dissipation intrinsic to the model. However, during seismic calculations, it may be useful for the user to know the energy dissipated that cannot be recovered. The variable dissip represents the accumulation of non-recoverable energy. The non-recoverable energy increment is written as \(\Delta \mathit{Eg}\mathrm{=}\frac{1}{2}(E(1\mathrm{-}{D}^{\text{+}})\Delta \varepsilon –({\sigma }^{\text{+}}\mathrm{-}{\sigma }^{\text{-}}))\Delta \varepsilon\).

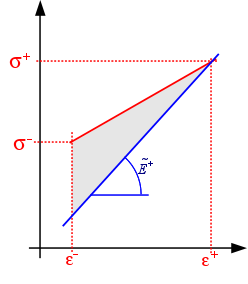
_images/10000000000000F80000011C7B6FB752D81B569F.png

Non-softening material

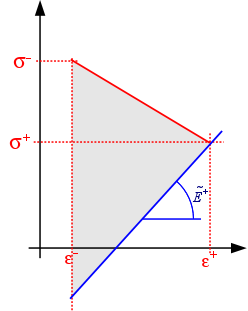
 _images/10000000000000F8000001372608D443230ECAF3.png

Softening material

The internal variables for Mazars’s law in \(\mathrm{1D}\):

\(\mathit{V1}\) CRITSIG: Criteria in constraint

\(\mathit{V2}\) CRITEPS: Deformation criterion.

\(\mathit{V3}\) ENDO: Damage [R7.01.08].

\(\mathit{V4}\) EPSEQT: Equivalent tensile deformation

\(\mathit{V5}\) EPSEQC: Equivalent compression deformation

\(\mathit{V6}\) RSIGMA: Tri-axiality ratio.

\(\mathit{V7}\) TEMP_MAX: Maximum temperature reached in the material

\(\mathit{V8}\) DISSIP: Non-recoverable energy.