9. Law of behavior RELAX_ACIER#

The relaxation phenomenon of steels used for prestress is regulated. The main regulations are: BPEL83, NF-EN-1992-1-1 October 2005, AFCEN - ETCC -2010,

We want to be able to model deformations that will vary slowly over time, in particular to take into account concrete creep and temperature variations. We also want to take into account the influence of temperature on the relaxation phenomenon.

Regularly, it would be possible to take into account the effect of concrete creep and thermal deformation by making a linear combination of the various phenomena (see regulations for more details). This approach is incompatible with a finite element calculation.

These regulations also make it possible to correct relaxation after a « jump » in deformation, which may be due to a variation in the stress resulting from external loading (for example during a ten-year test on an enclosure). In no case can this « jump » evolve over time, it can only be a Dirac. The method used in this case is that of equivalent time which, by construction, is incompatible with a finite element code.

9.1. Formulation of the model#

For the law of relaxation to be usable in a finite element code for structural calculations with load variations such as: concrete creep, cable tension recovery, taking into account the influence of thermal,… it must be incremental and thermodynamically correct.

Several formulations for modeling the deformation associated with relaxation exist in the literature.

The formulation adopted is based on that proposed by J.Lemaitre:

\(\mathrm{\sigma }=E.{\mathrm{\epsilon }}^{e}\) \(\mathrm{\epsilon }={\mathrm{\epsilon }}^{e}+{\mathrm{\epsilon }}^{\mathit{an}}\)

\({{\dot{\mathrm{\epsilon }}}^{\mathit{an}}=⟨\frac{\mathrm{\sigma }–R\left({\mathrm{\epsilon }}^{\mathit{an}}\right)}{{f}_{\mathit{prg}}.k}⟩}^{n}\) with \(R\left({\mathrm{\epsilon }}^{\mathit{an}}\right)=\frac{{f}_{\mathit{prg}}.c.{\mathrm{\epsilon }}^{\mathit{an}}}{{\left(1+{\left(b.{\mathrm{\epsilon }}^{\mathit{an}}\right)}^{\mathit{nr}}\right)}^{\frac{1}{\mathit{nr}}}}\) [éq9.1-1]

The law of behavior is 1D, and only available for bar-type models, which are used to model prestress cables in operator DEFI_CABLE_BP.

To take into account the influence of temperature on relaxation, all the coefficients of the law can be functions of temperature.

Note:

The parameters \(c\), \(b\), \(n\) and \(\mathit{nr}\) are unitless, and therefore independent of the units used during the study. \(k\) is dimensionless compared to \({f}_{\mathit{prg}}\) so in relation to the constraints, but not in relation to time. Indeed \({\dot{\mathrm{\epsilon }}}^{\mathit{an}}\) is homogeneous to \({[s]}^{-1}\), if the time unit is in seconds. So if we know \(k\) for a deformation rate in a unit of time, it is necessary to convert its value with respect to the unit of time used during the study.

9.2. Internal variables#

Two internal variables:

- \(V1\): the cumulative anelastic deformation: \({\mathrm{\epsilon }}^{\mathit{an}}\).

\(V2\): memorizing the stiffness tangent to the behavior.

9.3. Explicit integration#

The integration is carried out by a Runge-Kutta method of order five with variable steps.

9.4. Identifying parameters#

Several solutions are possible:

Analytical work makes it possible to determine relationships between the coefficients present in the regulatory formulas and that of the law of behavior: tangent at the beginning of relaxation, asymptote for an « infinite » time,…
Simulation of several « relaxation tests » using regulatory formulas. For a given cable type that corresponds to a set of parameters (k1, k2, \({\mathrm{\rho }}_{1000}\), \({f}_{\mathit{prg}}\)). Different values of \(\mathrm{\mu }\) will make it possible to obtain a « test » cluster on which an identification of the parameters can be carried out.
Bibliographical study to find the experimental and theoretical work carried out on the relaxation of prestress cables, in order to use the tests directly and to identify the parameters.

9.5. Result of an identification#

This identification was carried out in relation to the simulation of a relaxation test obtained with regulatory formulas.

We place ourselves in the case \({\mathrm{\rho }}_{1000}=2.5\text{\%}\) (\(k1=6.0E-03\), \(k2=1.1\)) with \({f}_{\mathit{prg}}=1800\mathit{MPa}\), \(E=190000\mathit{MPa}\). The initial deformation corresponds to a loading rate of \(\mathrm{\mu }=0.75\). Simulation and identification are carried out on [0h, 4000h].

The figures below compare the identification result with the regulatory curve.

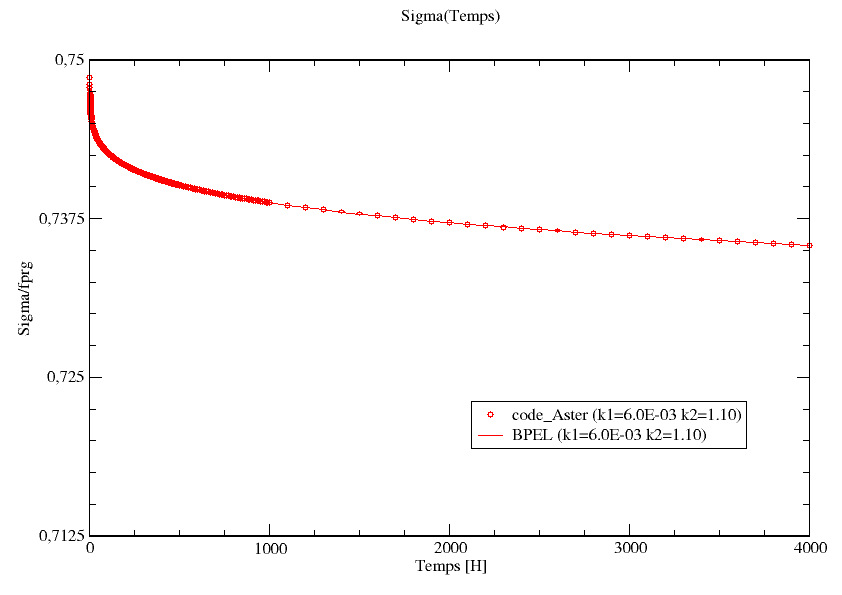
Figure 9.5-a: Evolution of the constraint over time: reference and code_aster.

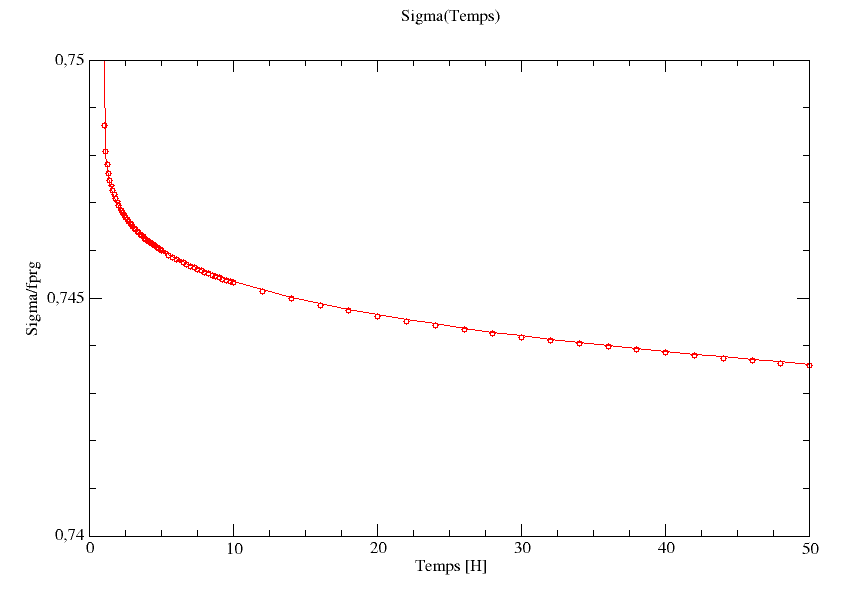
Figure 9.5-b: Focus on the first 10 hours, of the evolution of the stress over time.

Observations regarding identification:

Very good correspondence between the law identified and the regulatory law.
Very good identification of the original slope and the asymptote.

The proposed law is therefore capable of correctly describing the relaxation of a prestress cable, if its relaxation follows the regulatory curves.

9.6. Usage in code_aster#

The definition of the material parameters is done classically in the command DEFi_materiau, keyword RELAX_ACIER, all the parameters can depend on the temperature.

\({f}_{\mathit{prg}}\)	Cable breaking stress. This quantity is optional, as it can also be defined in materials BPEL_ACIERou ETCC_ACIERet in this case \({f}_{\mathit{prg}}\) is a constant. The value/function given under RELAX_ACIER_CABLest priority.
ECOU_K ECOU_N	Corresponds to the k coefficient in the equation. Corresponds to the coefficient n in the equation.
ECRO_N ECRO_B ECRO_C	Corresponds to the coefficient nr in the equation. Corresponds to the coefficient b in the equation. Corresponds to the coefficient c in the equation.



\({f}_{\mathit{prg}}\)	Cable breaking stress. This quantity is optional, as it can also be defined in materials BPEL_ACIER or ETCC_ACIER and in this case \({f}_{\mathit{prg}}\) is a constant. The value/function given under RELAX_ACIER_CABL takes precedence.
ECOU_K ECOU_N	Corresponds to the k coefficient in the equation. Corresponds to the coefficient n in the equation.
ECRO_N ECRO_B ECRO_C	Corresponds to the coefficient nr in the equation. Corresponds to the coefficient b in the equation. Corresponds to the coefficient c in the equation.