2. Newton’s method#
2.1. Principle of the method#
Newton’s method is a classical method for solving equations such as the search for zero. Consider a non-linear vector function \(F\) of the vector \(x\). We are looking for the zero of this function, that is to say:
Newton’s method consists in constructing a sequence of vectors \({x}^{n}\) converging on the solution \(x\). To find the new iterate \({x}^{n+1}\), we approach \(F({x}^{n+1})\) by expanding to order one around \({x}^{n}\) and we express that \(F({x}^{n+1})\) must be zero:
Or again:
Finally:
\({F}^{\text{'}}(x)\) is the tangent linear application associated with the \(F\) function. The derivative at point \(x\) in the \(h\) direction is defined as the following directional derivative:
The \({F}^{\text{'}}(x)\) matrix in the bases chosen for the vector spaces in question is called the Jacobian matrix of \(F\) at point \(x\). When \(F\) is a function of an Euclidean vector space with real values, \({F}^{\text{'}}(x)\) is a linear form, and we can show that there is a (unique) vector, denoted by \(\nabla F(x)\) and called the gradient of \(F\), such as:
That is, the dot product of \(h\) and the gradient of \(F\).
When we are close to the solution, the convergence of Newton’s method is quadratic, i.e. the number of zeros after the decimal point in the error doubles at each iteration (0.19 — 0.036 — 0.0013 — 0.0013 — 0.0000017 for example). But this method (using the true tangent) has several drawbacks:
It requires the calculation of the tangent at each iteration, which is all the more expensive the larger the size of the problem (especially in the case where a direct solver is used),
If the increment is large, the tangent (called coherent or consistent) may lead to discrepancies in the algorithm,
It may not be symmetric, which requires the use of specific solvers.
It is for this reason that other matrices can be used instead of the tangent matrix: the elastic matrix, a tangent matrix obtained previously, the symmetrized tangent matrix,…
2.2. Adapting Newton’s method to the problem posed#
Initially, the conditions at the Dirichlet limits are not taken into account. We must solve a system (non-linear because it depends on \({u}_{i}\)) of the form:
: label: eq-20
: label: eq-20
R ({u} _ {i}, {t} _ {i}) = {L} _ {i}) = {L} _ {i} ^ {L} _ {i} ^ {text {mecha}} ^ {text {mecha}}
Internal forces \({L}_{i}^{\text{int}}\) can symbolic be noted \({Q}_{i}^{T}\mathrm{.}{\sigma }_{i}\), where \({Q}_{i}^{T}\) is the matrix associated with the divergence operator (expression of the work of the virtual deformation field). Internal forces are then expressed:
And the forces of mechanical loading:
Where:
\({w}_{i}\) refers to the field of virtual travel;
\({f}_{i}\) refers to the volume forces applying at the moment \({t}_{i}\) to \(\Omega\);
\({t}_{i}\) refers to the surface forces applying at the moment \({t}_{i}\) on the border \(\Gamma\) of \(\Omega\).
The application of Newton’s method leads to the resolution of a series of linear problems of the type (\(n\) is the number of Newton’s iteration, \(i\) that of the instant variable):
Note \(\delta {u}_{i}^{n+1}={u}_{i}^{n+1}-{u}_{i}^{n}\) the displacement increment between two successive Newton iterations. Matrix \({K}_{i}^{n}\) is the tangent stiffness matrix in \({u}_{i}^{n}\) and the vector \({L}_{i}^{\text{int},n}\) represents the internal forces at the \({n}^{\text{ième}}\) Newton’s iteration of the \({i}^{\text{ème}}\) load step. Quantity \({R}_{i}^{n}=({L}_{i}^{\text{méca},n}-{L}_{i}^{\text{int},n})\) represents unbalanced forces, called the « balance residue. » The matrix \({K}_{i}^{n}\) is the matrix for the tangent linear application of the function \({R}_{i}^{n}\), so it is equal to:
In the absence of following forces [§ 3.2], the second term sucks. So all that remains of the matrix \({K}_{i}^{n}\) is the derivative at point \({u}_{i}^{n}\) of the internal forces with respect to the displacements:
A small error in the evaluation of internal forces can have serious consequences, because it is their exact calculation that guarantees, if we converge, that it will be towards the solution sought. On the other hand, it is not always necessary to use the true tangent matrix, which is expensive to calculate and factorize. For example, a variant of the method uses the elastic matrix \({K}_{\text{élas}}\). The method using the true tangent matrix \({K}_{i}^{n}\) (also called coherent or consistent matrix) is called the Newton method; methods using other matrices (such as the elastic matrix \({K}_{\text{élas}}\) for example) are called modified Newton methods or quasi-Newton methods. The choice between a tangent matrix (the last one obtained or a previous matrix) and an elastic matrix is made in Code_Aster using the keyword MATRICE = “TANGENTE” or MATRICE =” ELASTIQUE “of the keyword factor NEWTON. In addition, it is possible to use a discharge matrix, i.e. a matrix with constant internal variables (the evolution of nonlinearities is therefore not taken into account in this matrix), below a certain time step, for certain laws of behavior. Refer to the [U4.51.03] documentation for the use of this feature.
Newton’s method with a consistent tangent matrix can be illustrated simply using the diagram in d8.00.01-fig-newton.
We continue with the Newton iteration loop which allows, upon convergence, to obtain the values of \(\Delta {\mathrm{u}}_{i}\), and therefore those of \({\mathrm{u}}_{i}\) by applying equation ():
2.3. Euler prediction phase#
Experience shows that the convergence of Newton’s method is strongly dependent on a careful choice of the initial estimate: « the closer the initial estimate is to the solution, the faster the algorithm converges ». To start the iterative process of the method, it is therefore useful to determine a « good » initial increment \(\Delta {\mathrm{u}}_{i}^{0}\). To do this, we linearize the continuous problem with respect to time: this is what we call the prediction phase.
2.3.1. Linearization#
We will therefore linearize the system () with respect to the time around \({\mathrm{u}}_{i-1}\). We start by linearizing the internal forces \({L}_{i}^{\text{int}}\):
: label: eq-27
{L} _ {i} ^ {text {int}}}approx {L}}approx {L} _ {i-1} ^ {text {int}} + {frac {partial {L}} ^ {text {int}}} {text {int}}}} {text {int}}} {text {int}}} {text {int}}} {text {int}}}} {text {int}}}} {text {int}}}} {text {int}}}} {text {int}}}} {partial {int}}}} {partial u}mid}mid} Delta {u} _ {i} ^ {0} + {frac {delta {L} ^ {text {int}}} {delta t}mid} _ {{t}} _ {i-1}}
It is assumed that mechanical loading does not depend on time (subsequent loads are excluded), so:
By re-injecting and into the first equation of the system, we obtain for the equilibrium equation:
We have balance at moment \({t}_{i-1}\), that is to say:
: label: eq-30
{mathrm {L}} _ {i-1}} ^ {text {int}} = {mathrm {L}} _ {i-1} ^ {text {mecha}} ^ {text {mecha}}
And so what’s left is:
: label: eq-31
{frac {partial {mathrm {L}}} ^ {text {int}}} {partialmathrm {u}}mid} _ {mathrm {u}}} _ {i-1}}mathrm {.} Delta {mathrm {u}} _ {i}} ^ {0} + {frac {delta {mathrm {L}}} ^ {text {int}}}} {delta t}mid}mid}} _ {t} _ {i-1}}mathrm {.} Delta {t} _ {i} =Delta {mathrm {L}}} _ {i} ^ {text {mecha}} =Delta {text {mecha}}
We obtain the system of equations for calculating predictive values \(\Delta {\mathrm{u}}_{i}^{0}\):
: label: eq-32
{frac {partial {mathrm {L}}} ^ {text {int}}} {partialmathrm {u}}mid} _ {mathrm {u}}} _ {i-1}}mathrm {.} Delta {mathrm {u}} _ {i}} ^ {0} =Delta {mathrm {L}} _ {i} ^ {text {mecha}} - {frac {delta {delta {mathrm {L}}} ^ {text {L}}} ^ {text {int}}}} {delta t}mid} _ {i-1}} - {frac {delta {delta {mathrm {L}}}} ^ {text {int}}} {delta t}mid} _ {i-1}}mathrm {.} Delta {t} _ {i}
2.3.2. Tangent prediction matrix#
The quantity \({\frac{\partial {\mathrm{L}}^{\text{int}}}{\partial \mathrm{u}}\mid }_{{\mathrm{u}}_{i-1}}\) refers to the partial derivative at constant time of \({L}_{i-1}^{\text{int}}\), it can develop:
Matrix \({K}_{i-1}\) is called a tangent prediction matrix. The dependence of the matrix \(Q\) on displacements is neglected in the hypothesis of small displacements: the term \({\frac{\partial {Q}^{T}}{\partial u}\mid }_{{u}_{i-1}}\), called the geometric rigidity term, therefore disappears from. This term is taken into account for large transformations (see § 1.2.2). For developers, note that the calculation of the tangent matrix during the prediction phase is performed via calculation option RIGI_MECA_TANG.
2.3.3. Variants of the prediction#
There are other prediction options available in STAT_NON_LINE.
We can use an elastic matrix \({K}_{\text{élas}}\) in place of the tangent matrix in speed \({K}_{i-1}\), this is option PREDICTION =” ELASTIQUE “(option RIGI_MECA).
We can use a secant matrix \({K}_{\text{sécante}}\) in place of the tangent matrix in speed \({K}_{i-1}\), this is option PREDICTION =” SECANTE “(option RIGI_MECA_ELAS). The secant matrix is an elastic matrix whose Young’s modulus is used when applying damage (see for example [R5.03.18] for more details)
You can use a previously calculated displacement increment in place of the estimate, this is option PREDICTION =” DEPL_CALCULE “. In this case we do not do any system reversal and the \(\Delta {u}_{i}^{0}\) is directly given. See documentation [U4.51.03] for how to use it.
A displacement increment extrapolated from the previous step can be used. The estimate of the displacement increment is calculated from the total increment obtained as a solution to the previous time step (weighted by the ratio of the time steps). That’s option PREDICTION =” EXTRAPOL “.
In these last two cases, in order to ensure that the initial displacement is kinematically admissible, the estimate is projected onto all the kinematically admissible fields (i.e. satisfying the Dirichlet boundary conditions) according to the norm given by the elastic matrix, which must therefore be calculated.
2.3.4. Vector second member of control variables#
A command variable \(\beta (t)\) is a scalar quantity, a function of time and space [1] _ , given a prima facie by the user via the AFFE_VARC keyword in the AFFE_MATERIAU operator. It is a parameter of the problem and not an unknown. The quantity \({\frac{\delta {L}^{\text{int}}}{\delta t}\mid }_{{t}_{i-1}}\) refers to the partial differential, with respect to \(t\) and to the constant \(u\), of \({L}^{\text{int}}=Q\mathrm{.}\sigma (t,\beta (t))\). This particular notation is intended to draw attention to the fact that for \({n}_{\mathrm{varc}}\) command variables, we write the total differential:
If we take as an example the control variable describing the temperature \(\theta\):
It is assumed that the temperature varies linearly between the two moments:
The dependence of \(\sigma\) on time and on temperature makes it possible to write:
Because \(Q\) does not depend on time and therefore \(\frac{\delta }{\delta t}({Q}^{T})=0\). Vector \(\Delta {L}_{i}^{\text{varc}}\), whose expression is given by, is the temperature loading increment (watch out for the sign change!) that has been generalized to all control variables: temperature, irradiation, metallurgical phases (see [R4.04.02]),…
The explicit dependence of constraints on time is currently not taken into account and therefore the first term is equal to zero. And so finally:
The loading increment of the control variables \(\Delta {L}_{i}^{\text{varc}}\), resulting from the derivation of internal forces with respect to the control variables, is an estimate of the effect of a variation in the control variables.
In the case of temperature, if we note \(K\) the hydrostatic compression module and \(\alpha\) the thermal expansion coefficient, the thermal stress is written as:
Where \(I\) is the identity matrix. And so, by applying:
In the elastic case, these are the internal forces associated with thermal expansion (it is not strictly speaking a loading, it is rather similar to the effect of an initial deformation). This estimate is used in the prediction phase and in the stopping criterion. If thermal expansions cause the structure to leave the elastic domain (plasticity for example), this estimate will be corrected during Newton iterations.
2.3.5. Vector second member of mechanical loading#
The mechanic loading increment \(\Delta {\mathrm{L}}_{i}^{\text{méca}}\) is composed of dead loads (independent of geometry, such as gravity) and follower loads. In reality, there are cases (the first load increment, for example) where \({L}_{i-1}^{\text{méca}}\) is unknown. Recall that the loading increment () is written as:
We have balance at time \({t}_{i-1}\), so by applying:
Expressing the internal forces at the previous time step \({L}_{i-1}^{\text{int}}\) implies either saving this vector from the previous calculation if it exists (resuming a previous calculation), or integrating the law of behavior from the initial state given by the user (which can be expensive). For the sake of simplicity and efficiency, we choose not to reintegrate the law of behavior and we simply express the internal forces as the nodal forces by taking the constraints known at that moment, i.e.:
Hence the new expression:
The direct calculation from () asks the user to take care of the coherence between the field of constraints, the fields of displacement and internal variables (DEPL, SIGMet VARIdans ETAT_INIT). with respect to the integration of the law of behavior in the case of a resumption of calculation.
2.3.6. Linear system#
By re-injecting the expressions for \({\frac{\partial {L}^{\text{int}}}{\partial u}\mid }_{{u}_{i-1}}\) (equation), \({\frac{\delta {L}^{\text{int}}}{\delta t}\mid }_{{t}_{i-1}}\) (equation) and \(\Delta {L}_{i}^{\text{méca}}\) (equation) into, the system of equations in prediction is written:
2.4. Newton correction phase#
At the end of the prediction phase, we are left with an estimate of the displacement increment \(\Delta {u}_{i}^{0}\). If this estimate is accurate (modulo the application of the convergence criteria described in § 2.5), then we obtain the converge solution for the time step \({t}_{i}\):
But if this is not the case, we must find the value \(\Delta {\mathrm{u}}_{i}\) of the displacement increment from the value \({\mathrm{u}}_{i-1}\) obtained at the previous equilibrium (instant \({t}_{i-1}\)):
If the prediction phase has converged, we therefore have trivially:
Otherwise, we take \(\Delta {\mathrm{u}}_{i}^{0}\) as the initial value obtained at the end of the prediction phase, before correcting by the \(\delta {\mathrm{u}}_{i}^{n}\) iterations of the Newton method. With a sufficient number \({n}_{\mathrm{CV}}\) of Newton iterations (always with the arbitration of the convergence criterion):
: label: eq-50
{mathrm {u}} _ {i} ^ {text {converged}}} = {mathrm {u}} _ {i-1} +Delta {mathrm {u}} _ {i} ^ {0} ^ {0} +sum _ {j=1}} +sum _ {j=1}} ^ {j=1}} ^ {n= {n}} _ {mathit {CV}}}}delta {mathrm {u}}} _ {i} ^ {j}
As long as we have not converged (if Newton’s number of iterations is not sufficient), we note:
The total displacement, for the time step \(i\) and the Newton iteration \(n\), will therefore be written as:
: label: eq-52
{mathrm {u}} _ {i} ^ {n} = {mathrm {u}} _ {i-1} +Delta {mathrm {u}}} _ {i} ^ {n} _ {i} ^ {n}
At each iteration, we must solve a system to determine \(\delta {\mathrm{u}}_{i}^{n}\), the increments of the movements since the result \({\mathrm{u}}_{i}^{n-1}\) of the previous iteration:
We also note:
Or again:
2.4.1. Linearization#
We must linearize the system () with respect to the unknowns by \({\mathrm{u}}_{i}^{n}\) to \({t}_{i}\) being constant. We start by linearizing the internal forces \({L}_{i}^{\text{int},n}\):
It is assumed that mechanical loading does not depend on time (subsequent loads are excluded).
2.4.2. Linear system#
By re-injecting () into equation (), we obtain for the equilibrium equation:
The quantity \({\frac{\partial {L}^{\text{int}}}{\partial u}\mid }_{{u}_{i}^{n-1}}\) is called a coherent tangent matrix and it is denoted \({K}_{i}^{n-1}\):
The system to be solved is finally written:
The internal force vector \({L}_{i}^{\text{int},n-1}\) is calculated using the constraints \({\sigma }_{i}^{n-1}\). These are calculated from the \({\mathrm{u}}_{i}^{n-1}\) displacements through the material behavior relationship [§ 1.1]. In fact, in the case of incremental behaviors, \({\sigma }_{i}^{n-1}\) is calculated from \(({\sigma }_{i-1},{\alpha }_{i-1})\) and the deformation increment \(\epsilon (\Delta {\mathrm{u}}_{i}^{n-1})\) induced by the displacement increment since the start of the iterative process (including the prediction phase) or by the transformation gradient \(\mathrm{F}\) in the case of large transformations.
2.4.3. Difference between matrices in prediction and correction#
It is important to emphasize that the tangent matrix from option RIGI_MECA_TANG (prediction phase) and the tangent matrix from option FULL_MECA (correction phase) are in general not identical. Assume that we have reached convergence for the moment \({t}_{i-1}\) and that we are now looking for equilibrium for the next moment \({t}_{i}\). The matrix resulting from RIGI_MECA_TANG comes from a linearization of the equilibrium equations with respect to time around \(({u}_{i-1},{\lambda }_{i-1})\) i.e. around the equilibrium at time \({t}_{i-1}\). So it’s the tangent matrix of the converged system at time \({t}_{i-1}\).
On the other hand, the matrix from FULL_MECA comes from a linearization of the equilibrium equations in relation to the displacement around \({\mathrm{u}}_{i}^{n}\) i.e. around the equilibrium at the time \({t}_{i}\).
The differences between RIGI_MECA_TANG and FULL_MECA can be interpreted in other words. We can thus show that the matrix from RIGI_MECA_TANG corresponds to the tangent operator of the continuous problem in time, also called the speed problem (and relates the stress rate to the deformation rate), while the matrix from FULL_MECA corresponds to the tangent operator of the discretise problem in time. Document [R5.03.02] gives the expression in each of the two cases for the Von Mises elasto-plasticity relationship with isotropic or linear kinematic work hardening.
We recall that the treatment of a behavioral relationship [R5.03.02 § 5] consists in:
Calculate the constraints \({\sigma }_{i}^{n}\) and the internal variables \({\alpha }_{i}^{n}\) from the initial state \(({\sigma }_{i-1},{\alpha }_{i-1})\) and the deformation increment \(\varepsilon (\Delta {u}_{i}^{n-1})\) induced by the displacement increment since the start of the iterative process (including the prediction phase).
Calculate internal forces \({L}_{i}^{\text{int},n}={Q}_{i}^{T}\mathrm{.}{\sigma }_{i}^{n}\).
Calculate (possibly) the tangent matrix (option RIGI_MECA_TANG for the prediction phase, option FULL_MECA for Newton iterations).
2.5. Convergence criteria#
At the end of the prediction and at each Newton’s iteration, one must estimate whether the iterative process has converged (the balance of the structure is reached). We use the current time step \({t}_{i}\) and the Newton iteration \(n\) (provided that the value \(n=0\) corresponds to the prediction). There are four convergence criteria.
Criterion RESI_GLOB_MAXI is to check that the infinite norm [2] _ of the residue is less than the \(\gamma\) value specified by the user.
It is not advisable to use this criterion alone, as it is not easy to get an idea of the absolute allowable orders of magnitude.
Criterion RESI_GLOB_RELA (chosen by default) amounts to verifying that the residue is sufficiently small, as before, and this in relation to a quantity representative of the load.
: label: eq-61
frac {{parallel {mathrm {Q}}} ^ {T}text {.} {sigma} _ {i} ^ {n} - {mathrm {L}} - {mathrm {L}}} _ {text {mecha}}parallel}} {{parallel {mathrm {L}} - {mathrm {L}}} - {mathrm {L}}}} {parallel {mathrm {L}}}} {{parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel parallel} _ {infty}}leeta
\(\eta\) being the desired relative precision given by the user under the RESI_GLOB_RELA keyword (or the default value of \({10}^{\text{-6}}\)).
Note that, in the case of using RESI_GLOB_RELA, the criterion may become singular if the external load \({\mathrm{L}}_{i}^{\text{méca}}+{\mathrm{L}}_{i}^{\text{varc}}\) becomes zero. This can happen in case of total discharge of the structure. If such a scenario occurs (i.e. load \({10}^{\text{‑6}}\) times smaller than the smallest load observed up to the present increment), the code then uses the RESI_GLOB_MAXI criterion with the value that observed at the convergence of the previous increment as a value. When the load becomes non-zero again, we return to the initial criterion.
The third criterion is criterion RESI_REFE_RELA: the idea of this criterion is to build a nodal reference force, which will be used to estimate, term by term, the (approximate) nullity of the residue:
: label: eq-62
forall jinleft{text {ddl}right}right}mid {left ({mathrm {Q}}} ^ {T}text {ddl}text {ddl}right}right}mid {left ({mathrm {Q}}} ^ {T}}text {. {sigma} _ {i} ^ {n} - {mathrm {L}} - {mathrm {L}}} _ {text {mecha}}right)} _ {j}midmidleleepsilontext {.} {mathrm {F}} _ {j}} ^ {text {ref}}
More precisely, the reference nodal force \({\mathrm{F}}_{j}^{\text{ref}}\) is constructed from the data of a reference amplitude \({A}^{\text{ref}}\) which can be:
A constraint;
One pressure, one temperature in the case of THM;
Generalized strength in the case of beams or shells;
others…
The list is available in the documentation for using the STAT_NON_LINE [U4.51.03] command, description of the RESI_REFE_RELA operand.
If we take a constraint as an example, the reference amplitude \({\sigma }^{\text{ref}}\) being given by the user via the SIGM_REFE keyword. From this reference stress amplitude, the tensor \({\sigma }^{\text{test}}\) is defined: it is zero for all these components, except the j -th which is equal to \({\sigma }^{\text{ref}}\). We then define, for each node of each element, the nodal force \({\tilde{R}}_{i}^{e}\) (the aim being to give an idea of the importance of a component at a Gauss point of the stress on the nodal force):
With \(N\) the number of Gauss points in the element, \(M\) the number of components of the stress tensor; the exponent \(\alpha\) used to note the quantity evaluation at the Gauss point. For example \({\omega }^{\alpha }\) are the weights of Gauss points.
Note: For some elements, such as bars, grids, or membranes, this definition results in zero reference residuals on some axes. To remedy this, the nodal reference forces are determined via an order of magnitude calculation based on the size of the element.
The reference nodal force is then defined by:
where \({\Gamma }_{i}\) is the set of elements connected to node \(i\).
The fourth criterion is criterion RESI_COMP_RELA: the idea of this criterion is to separate the different contributions of the residue components by components (in the sense DX, DY, DZ, PRE1, PRE2, TEMP). Each of the vectors obtained will then be normalized by the internal force corresponding to this residue. This choice of convergence criteria only makes sense for highly evolving problems, typically problems THM. Moreover, this choice will be effective when there are problems with strong contrasts. Indeed, it is the « high gradient » areas that will control convergence. We define \({F}^{n}(c)\) the part of the \({\mathrm{Q}}^{T}\text{.}{\sigma }_{i}^{n}-{\mathrm{L}}_{i}^{\text{méca}}\) residue corresponding to the component \(c\) and \({\mathrm{L}}^{\text{int}\mathrm{,0}}(c)\) the vector of internal forces in prediction corresponding to this same component \(c\). Criterion RESI_COMP_RELA then comes down to verifying that this residue is sufficiently small, that is to say:
Convergence is declared achieved when all the criteria specified by the user are verified simultaneously. By default, we test the relative global residue (RESI_GLOB_RELA) and the maximum number of Newton iterations (ITER_GLOB_MAXI).
For residues RESI_GLOB_RELA and RESI_GLOB_MAXI, all the components of the displacement field are used in the evaluation of standard \({\mathrm{\parallel }\mathrm{.}\mathrm{\parallel }}_{\mathrm{\infty }}\), except in two cases where a particular treatment is made in terms of the choice of components:
For loads of type AFFE_CHAR_CINE, the degree of freedom concerned is ignored in the evaluation of the residue norm because the procedure for eliminating unknowns does not allow access to support reactions;
For continuous contact, the components LAGR_C and LAGR_F1/LAGR_F2 are ignored in the evaluation of the norm because the Signorini-Coulomb law is already verified in the algorithm (see [R5.03.52]) and these terms are dimensionally inconsistent with those relating to movements; on the other hand, for the case of contact in XFEM, these components are retained because they serve to verify the condition LBB;
2.6. Use of a tangent-secant evolutionary matrix#
The method described in this paragraph applies exclusively to highly non-linear problems, where a classical Newton method fails for any type of matrix choice, for the prediction or correction phase. Typically, the usual Newton method is flawed for poorly posed problems arising from the use of softening laws of behavior (see for example R5.04.01).
In these situations, non-convergence occurs when the algorithm is unable to choose between several admissible solutions, in a given (nickname) -time increment. This lack of convergence at the global level is most often reflected at the local level (i.e. at the point of integration) by a repeated alternation between a non-dissipative state (elastic) and a dissipative state (plasticity, damage,…) during consecutive Newton iterations.
One of the strategies consists in using the concept of piloting (see R5.03.80) to overcome Newton’s shortcomings. The other strategy is to change the tangent matrix. It is this last strategy that is detailed here.
By tracking the status of each integration point from one iteration to the next, we can identify the points responsible for global non-convergence. Once these points have been identified, we decide to modify the matrix in the hope that this modification will allow global convergence.
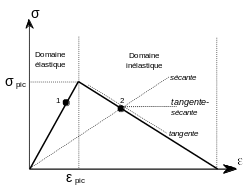
Figure 2‑2.6-a: Softening behavior law, use of a mixed tangent-secant matrix
The approach called tangent-secant, activated under the keyword COMPORTEMENT with TANGENTE_SECANTE =” OUI “, is justified by the following reasoning: if Newton’s method using the coherent tangent matrix does not converge, it is often because a certain number (variable) of integration points changes state (non-dissipative/dissipative) between two global Newton iterations. At the local level (see Figure 2-2.6-a), this means that we continue to alternate between domain 1 (\(\varepsilon <{\varepsilon }_{\text{pic}}\)) and domain 2 (\(\varepsilon >{\varepsilon }_{\text{pic}}\)). Because of the change in slope between 1 and 2, the use of a coherent secant or tangent matrix leads to a very poor approximation, which is why it is interesting to modify it. The choice presented consists in constructing the tangent matrix as a linear combination between the coherent tangent matrix and the secant matrix, both being determined by the laws of behavior. Currently, the approach is only available for softening behavior law ENDO_ISOT_BETON.
To manage the priming of the tangent-secant option, we introduce an additional internal variable compared to the existing internal variables, \(\alpha =({\alpha }_{1},\dots {\alpha }_{n},{\alpha }_{n+1})\) (with \(n\) the number of internal variables of the model used). This variable reflects the possible alternation between the elastic state and the softening state of a Gauss point. It is initialized at the first Newtonian iteration of each new time step, then it is changed to know, at each Gauss point, the number of successive alternations between the two states. With this information, we can estimate that from a certain threshold (for example \({S}_{0}=3\) alternations), Newton’s algorithm will no longer be able to converge for the current time increment and that it is necessary to modify the tangent matrix. To modify the matrix, we rely directly on how the coherent tangent matrix in ENDO_ISOT_BETON is constructed (see [R7.01.04]). It is a question of making the sum between the dissipative part and the non-dissipative part.
where \({K}_{\text{tg}}\) is the tangent matrix, \({K}_{\text{sc}}\) the secant matrix (non-dissipative part) and \({K}_{\text{end}}\) the damaging correction (dissipative part). For the modified matrix \({K}_{\text{t-s}}\), we replace the expression \({K}_{\text{tg}}\) in () by:
where \(\eta\) is a \({\alpha }_{n+1}\) function with values between 0 and 1. The function \(\eta\) selected in the following is as follows:
where \(A\) is a constant and \({S}_{0}\) the threshold on the value of the number of successive alternations undergone from which the tangent matrix is modified. For \({\alpha }_{n+1}={S}_{0}\) the matrix remains coherent tangent and for \({\alpha }_{n+1}\gg {S}_{0}\), it becomes secant. Values considered satisfactory for these parameters are \(A=\mathrm{1,5}\) and \({S}_{0}=3\) (values by default). The choice on the evolution of the value of \({\alpha }_{n+1}\) is essential for the performance of the algorithm. We choose an increase of \({\alpha }_{n+1}\) by \(G=\mathrm{1,0}\), \({\alpha }_{n+1}\to {\alpha }_{n+1}+G\) for each new alternation between an elastic state and a damaging state, then a decrease of \({\alpha }_{n+1}\) by \(P\), \({\alpha }_{n+1}\to {\alpha }_{n+1}-P\), when the state remains damaging twice in a row. The objective of using \(P\) is to allow the return to the coherent tangent matrix when a Gauss point remains damaging over several iterations, since the coherent tangent matrix makes the convergence quadratic, provided we are close to the solution. The value of the rate of decrease \(P\) compared to the rate of increase \(G\), is crucial for the behavior of the evolutionary algorithm. The overall idea is to increase \({\alpha }_{n+1}\), when you are far from the solution to have an operator closer to the secant than to the coherent tangent, then once « close » to the solution, to switch to a coherent tangent matrix (which is the best in Newton’s sense). The \(P/G\) ratio (keyword TAUX_RETOUR — 0.05 by default) represents the third parameter of the algorithm, in addition to \(A\) (keyword AMPLITUDE). and \({S}_{0}\) (SEUIL keyword).
2.7. Newton-Krylov method#
2.7.1. General principle#
The Newton-Krylov method is one of Newton’s inaccurate methods. It can only be used when the linear system solver () is iterative (as opposed to a direct solver). This approach does not change the choice of the system’s tangent matrix like the previous methods. It plays on the convergence criterion of the iterative solver used for the linearized system. By adapting the convergence criterion of the iterative method as best as possible to Newton’s convergence, we avoid doing unnecessary iterations (in the linear solver) and we thus gain in calculation time.
2.7.2. Implementation#
The general principle of inaccurate Newton methods is to replace the condition that solution increment \(\delta {\mathrm{u}}_{i}^{n}\) is the exact solution of the system () with a weaker condition. We ask that \(\delta {\mathrm{u}}_{i}^{n}\) check the condition:
where \({\eta }_{n}\) is called the forcing term.
We can show that the proposed method is convergent and that when the sequence \({\eta }_{n}\) tends to \(0\), the convergence is super-linear (see [8] p.96). The smaller this value, the closer the solution will be to that obtained by an exact resolution, but the less time will be saved in resolving the linear system. It is therefore necessary to find a good compromise between solving linear systems quickly and not to excessively degrade the convergence of Newton iterations.
Examining condition (), we see that it is identical to the criterion of relative convergence of the iterative solvers used to solve the linearized Newton system. To verify this condition, it is therefore a question of using the forcing term as the convergence criterion of an iterative linear solver.
As we saw previously, it is also necessary to ensure that the sequence \({\eta }_{n}\) tends to \(0\) to maintain the super-linear convergence of Newton’s method. To do this, we will subjugate \({\eta }_{n}\) to the decrease of the Newton residue by the law of evolution (cf. [8] p.105):
where the constant is chosen such as \(\gamma =0.1\).
This simple formula is not sufficient in practice because it is necessary to ensure an adequate decrease of \({\eta }_{n}\). To do this, we completely determine \({\eta }_{n}\) by the following expression:
: label: eq-71
{eta} _ {n+1} ={begin {array} {ccc} {eta} _ {0} & n=-1&\ mathit {max} (mathit {min} (0.4 {eta} _ {n} _ {n} _ {n}, {n}}, {eta} _ {n}}, {eta} _ {n}}, {eta} _ {n}, {n}}, {eta} _ {n}, {n}}, {eta} _ {n}, {n}}, {eta} _ {n}, {n}}, {eta} _ {n}, {n}, {n}}, {eta} _ {n}, {n}}, {eta} _ {n}, {n}mathrm {0,} & (1-gamma) {eta}} {eta} _ {n} _ {n} _ {gamma) {eta} _ {n},mathit {max} ({eta} max} ({eta}} _ {n+1} _ {n+1}) ^ {n+1} ^ {n+1} ^ {n+1} ^ {2} ^ {2}), (1-gamma) {eta} _ {n} _ {n},mathit {max} (max}) ({eta} max} ({max}) ({eta}) & nmathrm {0,} & (1-gamma) {gamma) {eta} _ {n} ^ {2} >0.2end {array}
where the constant is \({\eta }_{0}=0.9\) and corresponds to the convergence criterion used for the first linear resolution.
\({\eta }_{\mathit{min}}\), in turn, is the value of the convergence criterion of the iterative linear solver provided by the user (keyword RESI_RELA).