3. Limit conditions and loads#
3.1. Classification#
In the following paragraphs, we will describe all the possible loads in the operator and their classification. First of all, it is necessary to distinguish three main categories of loads:
Dirichlet loadings (boundary conditions) apply to nodal unknowns in a broad sense: it can be a displacement, a temperature or a pressure (for THM). They can be applied by elimination (AFFE_CHAR_CINE) or by dualization (AFFE_CHAR_MECA). When the boundary conditions are treated by elimination, they are taken into account when solving the linear system, internally and therefore does not modify the equations already described above in any way;
Neumann loads generally apply to flows. These are force conditions, in general, defined on the meshes (except for loading FORCE_NODALE).
There is another distinction to be made between following loads and those that are not. A load is follower when it depends on the geometry of the structure. Typically, the pressure is exerted in the opposite direction than normal. Therefore, when the structure deforms with the evolution of the load, the load, expressed in an absolute coordinate system, is transformed. There are also follower Dirichlet loadouts. These are boundary conditions that depend on geometry because they are non-linear. Loads that do not depend on the geometry of the structure are called dead or fixed loads (for example, gravity).
3.2. Follower loads#
To indicate that a load should be treated as a trailing load in STAT_NON_LINE, we specify TYPE_CHARGE =” SUIV “under the keyword EXCIT. A mechanical load \({L}^{\text{méca}}({u}_{i})\) comprising follower loads is therefore divided into two parts:
The exponent \({}^{\mathrm{fixe}}\) here refers to dead charges, and \({}^{\text{suiv}}\) refers to subsequent charges. The system of equations to be solved then becomes:
The derivation operations making it possible to write the prediction phase and the iterations of the Newton method therefore involve the derivatives of \({L}_{i}^{\text{méca}}({u}_{i})={L}_{i}^{\text{fixe}}+{L}_{i}^{\text{suiv}}({u}_{i})\) with respect to the movements \(({u}_{i})\). The prediction phase becomes:
And Newton’s iterations are about solving the system:
Thus, at the start of each load step (prediction) and at each Newton’s iteration, we must calculate a stiffness matrix \({\frac{\mathrm{\partial }{\mathrm{L}}^{\text{suiv}}}{\mathrm{\partial }\mathrm{u}}\mathrm{\mid }}_{\mathrm{u}}\) and a vector \({L}^{\text{suiv}}\) linked to the follower loadings.
The only Neumann loads that can be treated as follow-up loads in the current state of operator STAT_NON_LINE are:
The pressure for 3D models, 3D_SI, D_ PLAN, D_, D_, D_ PLAN_SI, D_, AXIS, AXIS_SI, C_ PLAN, C_ PLAN_SI [R3.03.04] and COQUE_3D [R3.03.07];
The gravity load for elements CABLE_POULIE [R3.08.05], elements with three knots comprising a pulley and two cable straps: the force of gravity exerted on the element depends on the respective lengths of the two wires;
The centrifugal force in large displacements, which for a rotation speed \(\omega\) is given by: \({\int }_{\Omega }\rho \text{.}\omega \wedge \left[\omega \wedge \text{OM}\right]\text{.}d\Omega ={\int }_{\Omega }\rho \text{.}\omega \wedge \left[\omega \wedge ({\text{OM}}_{0}+u)\right]\text{.}d\Omega\). Available for 3D models and AXIS_FOURIER;
The gravity load for all THM models of unsaturated porous media [R7.01.10]: in fact, the density depends on nodal variables to take into account the behavioral relationships of geomaterials.
3.3. Dualized boundary conditions — Linear case#
We will now take into account the dualized boundary conditions when writing the linear system to be solved. At first, we are only going to consider linear relationships. It is assumed the existence of a potential \(J(v)\) such that the minimization of the latter makes it possible to express the mechanical balance (in the weak sense) of the structure. If \(J(u)\) is this minimum then we have:
\({L}^{\text{int}}(u,v)\) refers to the sum of discretized internal forces. It depends on the solution sought via the laws of behavior, the kinematics of large transformations, etc.
\({L}^{\text{ext}}(u,v)\) refers to the sum of discretized external forces. It may depend on the solution as in the case of succeeding forces, contact, etc.
\(V\) refers to all eligible test solutions;
\(U\) refers to all eligible solutions sought;
:math:`B` is a*linear operator of the space of the fields of movements on a space of functions defined on a part of the edge of the structure;
Note: in mechanics, we can consider the presence of dissipative forces related to the viscous nature of the law of behavior or to the forces of friction. In these cases the potential is replaced by the existence of a pseudodissipation potential. We do not go into details but we show that we can bring ourselves back into the framework of an optimization problem thanks to the Legendre-Fenchel transformation. For the sake of simplicity, we keep the general framework of the previous equation because the rest of the developments is not impacted by the existence of a pseudo-potential.
In discrete form, the dualization of Dirichlet boundary conditions \(\mathrm{B}\mathrm{.}\mathrm{u}={\mathrm{u}}^{d}(t)\) leads to the following problem [R3.03.01]:
The unknowns are now, at all times \(t\) * , the \((u,\lambda )\) couple, where \(\lambda\) represents the Lagrange multipliers of the Dirichlet boundary conditions [R3.03.01]. Vector \({B}^{T}\text{.}\lambda\) is interpreted as the opposite of support reactions at the corresponding nodes. By setting by instant \({t}_{i}\):
Finding balance therefore consists in cancelling in \(({u}_{i},{\lambda }_{i},{t}_{i})\) the residual equilibrium vector which will be defined by:
The unknowns are calculated incrementally by the global resolution algorithm including the Lagrange multipliers of the dualized boundary conditions. Starting with \(({u}_{i-1},{\lambda }_{i-1})\), a solution satisfying the balance in \({t}_{i-1}\), we determine \(\Delta {u}_{i}\) and \(\Delta {\lambda }_{i}\) which will make it possible to obtain the solution in \({t}_{i}\):
3.3.1. Euler prediction phase#
For prediction, it is always necessary to linearize the system () with respect to time but, in this case, around the two unknowns (displacements and Lagrange multipliers) \(({u}_{i-1},{\lambda }_{i-1})\). We first note that the linearization of support reactions \({B}^{T}\text{.}{\lambda }_{i}\) is immediate because linear boundary conditions are considered and therefore the matrix \(\mathrm{B}\) is constant (it does not depend on displacements or time). Like \({\lambda }_{i}=\Delta {\lambda }_{i}^{0}+{\lambda }_{i-1}\), it comes immediately:
: label: eq-81
{mathrm {B}} ^ {T}mathrm {.} {lambda} _ {i} = {mathrm {B}}} ^ {T}mathrm {.} Delta {lambda} _ {i} ^ {0} + {mathrm {B}}} ^ {T}mathrm {.} {lambda} _ {i-1}
It is assumed that mechanical loading does not depend on time (subsequent loads are excluded) and that the Dirichlet limit conditions are also linear, so:
: label: eq-82
{begin {array} {c} {mathrm {L}}} _ {i}} _ {i} ^ {text {mecha}} = {mathrm {L}}} _ {i-1} ^ {text {mecha}} ^ {text {mecha}} ^ {mathrm {u}}}} +\ text {mecha}} ^ {text {mecha}} ^ {mathrm {u}}}} +Delta {mathrm {L}}} +Delta {mathrm {L}}} +Delta {mathrm {L}}} +Delta {mathrm {L}}} _ {i} _ {i}} ^ {d} = {mathrm {u}}} _ {i-1} ^ {d} +Delta {mathrm {u}} _ {i} ^ {d}end {array}
For the equilibrium equation, we obtain:
: label: eq-83
{mathrm {L}} _ {i-1}} ^ {text {int}} ^ {text {int}} ^ {text {int}}}} {partialmathrm {u}} ^ {partialmathrm {u}}}mid}} _ {mathrm {u}}} _ {i-1}}mathrm {.} Delta {mathrm {u}} _ {i}} ^ {0} + {frac {delta {mathrm {L}}} ^ {text {int}}}} {delta t}mid}mid}} _ {t} _ {i-1}}mathrm {.} Delta {t} _ {i} + {mathrm {B}}} ^ {T}mathrm {.} Delta {lambda} _ {i} ^ {0} + {mathrm {B}}} ^ {T}mathrm {.} {lambda} _ {i-1} = {mathrm {L}}} _ {i-1} ^ {text {mecha}} +Delta {mathrm {L}}} _ {i}} _ {i}} ^ {i} ^ {text {mecha}}
We have balance at moment \({t}_{i-1}\), that is to say:
And so what’s left is:
If we now look at the second equation of the system (), we get for the Dirichlet boundary conditions:
We have balance at moment \({t}_{i-1}\), that is to say:
: label: eq-87
mathrm {B}mathrm {.} {mathrm {u}} _ {i-1} = {mathrm {u}} _ {i-1} ^ {d}
In the end, there is:
: label: eq-88
mathrm {B}mathrm {.} Delta {mathrm {u}} _ {i} ^ {0} =Delta {mathrm {u}} _ {i}} ^ {d}
We obtain the system of equations for calculating predictive values \((\Delta {\mathrm{u}}_{i}^{0},\Delta {\lambda }_{i}^{0})\):
It will then be noted that this expression now involves the Lagrange multipliers at the previous instant, which are sometimes unknown (at the first load increment, for example). This means that with this new expression, we have moved the problem of knowing internal forces at the moment \({t}_{i-1}\) to ignoring the Lagrange multipliers at this same moment! But because the boundary conditions are linear, the problem is simplified. Consider that the solution of () with respect to Lagrange multipliers \({\stackrel{ˆ}{\lambda }}_{i}\) is written in incremental form:
This solution solves the first equation of the system:
: label: eq-91
{K} _ {i-1}mathrm {.} Delta {u} _ {i} ^ {0} + {B} ^ {T}mathrm {.} {Deltastackrel {} {lambda}}} _ {i} ^ {0}} = {L} _ {i} ^ {text {mecha}} - {Q} _ {i-1} _ {i-1}} ^ {1} ^ {T}mathrm {.} {sigma} _ {i-1} - {B} ^ {T}mathrm {.} {stackrel {} {lambda}}} _ {i-1}} +Delta {L} _ {i} ^ {text {varc}}
The idea is to look for that \({\stackrel{ˆ}{\lambda }}_{i}\). As the operator \({B}^{T}\) is constant, by applying, we have:
: label: eq-92
{K} _ {i-1}mathrm {.} Delta {u} _ {i} ^ {0} + {B} ^ {T}mathrm {.} {stackrel {} {lambda}} _ {i}} _ {i} = {L} _ {i} ^ {text {mecha}} - {Q} _ {i-1} ^ {1} ^ {T} ^ {T}mathrm {.} {sigma} _ {i-1} +Delta {L} _ {i} ^ {text {varc}} +Delta {L}}
It is assumed that the boundary conditions are met, so:
The required trips can also be written in incremental form:
The matrix \(B\) is constant, so at the previous increment we had (the problem has been resolved):
Using and in:
At equilibrium, we therefore have \({\stackrel{ˆ}{\lambda }}_{i}\) which also meets the limit conditions that we rewrite:
The Lagrange multipliers vector \({\stackrel{ˆ}{\lambda }}_{i}\) can therefore be found during the prediction phase by modifying the equation for imposing the boundary conditions with the expression. By analogy with the increment of the displacements found in prediction \(\Delta {u}_{i}^{0}\) we will note \(\Delta {\lambda }_{i}^{0}={\stackrel{ˆ}{\lambda }}_{i}\):
A particular case concerns the use of an excitation of the type TYPE_CHARGE = “DIDI” meaning Dirichlet differential, i.e. with respect to the initial state. For block-type boundary conditions, this consists in imposing, not step \(B\text{.}u={u}^{d}\), but \(B\text{.}(u-{u}_{\text{didi}})={u}^{d}\) In this case, the system to be solved in the prediction phase for the new load increment is:
3.3.2. Newton correction phase#
We must linearize the system with respect to the unknowns by \(({u}_{i}^{n},{\lambda }_{i}^{n})\) to \({t}_{i}\) being constant. We start by linearizing the internal forces \({L}_{i}^{\text{int},n}\):
: label: eq-100
{L} _ {i} ^ {text {int}, n}approx {L} _ {i} ^ {i} ^ {text {int}, n-1} + {frac {partial {L} ^ {text {int}} ^ {text {int}}}} {text {int}}}} {text {int}} ^ {int} ^ {L} ^ {L} ^ {L} ^ {L} ^ {text {int}} ^ {int} ^ {L} ^ {text {int}} ^ {int} ^ {L} ^ {text {int}}} {text {int}}} {text {int}}} {text {int}}} {text { delta {u} _ {i} ^ {n}
The linearization of support reactions \({B}^{T}\text{.}{\lambda }_{i}^{n}\) is immediate (linear conditions):
: label: eq-101
{B} ^ {T}mathrm {.} {lambda} _ {i} ^ {n} = {B} ^ {T}mathrm {.} {lambda} _ {i} ^ {n-1} + {B} ^ {T}mathrm {.} delta {lambda} _ {i} ^ {n}
It is assumed that mechanical loading does not depend on time (subsequent loads are excluded) and that the Dirichlet boundary conditions are also linear. For the equilibrium equation, we obtain:
: label: eq-102
{L} _ {i} ^ {text {int}, n-1} + {frac {partial {L} ^ {text {int}}} {partial u}mid} _ {{u} _ {u} _ {i} _ {i} ^ {n-1}}}mathrm {.} delta {u} _ {i} ^ {n} ^ {n} + {B} ^ {T}mathrm {.} {lambda} _ {i} ^ {n-1} + {B} ^ {T}mathrm {.} delta {lambda} _ {i} ^ {n} = {L} _ {i} ^ {text {mecha}}
For the boundary conditions, the linearization of the system () gives us analogous to:
: label: eq-103
Btext {.} delta {u} _ {i} ^ {n} = {u} _ {i} ^ {d} -Btext {.} {u} _ {i} ^ {n-1}
The system to be solved is finally written:
: label: eq-104
{begin {array} {c} {mathrm {K}}} _ {i} ^ {n-1}mathrm {.} delta {mathrm {u}} _ {i}} ^ {n} + {mathrm {B}} ^ {T}mathrm {.} delta {lambda} _ {i} ^ {n} = {mathrm {L}}} _ {i} ^ {text {mecha}} - {mathrm {L}} _ {i}} _ {i} ^ {i} ^ {text {int} ^ {int} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {i} ^ {text {int}, n-1} - {text {int}, n-1} - {mathrm {B}} ^ {T}mathrm {.} {lambda} _ {i} ^ {n-1}\ mathrm {B}text {.} delta {mathrm {u}} _ {i}} ^ {n} = {mathrm {u}} _ {i} ^ {d} -mathrm {B}text {.} {mathrm {u}} _ {i}} ^ {n-1}end {array}
3.3.3. Adaptation of convergence criteria#
Here we explain the adaptation of RESI_GLOB_MAXI and RESI_GLOB_RELA to the case of dualized boundary conditions. Criterion RESI_GLOB_MAXI is to check that the infinite norm of the residue is less than the \(\gamma\) value specified by the user. It is necessary to introduce the contribution of dualized boundary conditions:
: label: eq-105
{parallel {mathrm {Q}}} ^ {T}mathrm {.} {sigma} _ {i} ^ {n} + {mathrm {B}} ^ {T}mathrm {.} {lambda} _ {i} ^ {n} +- {mathrm {L}} _ {i} ^ {text {mecha}}parallel} _ {infty} _ {infty}legamma
Criterion RESI_GLOB_RELA (chosen by default) amounts to verifying that the residue is sufficiently small, as before, and this in relation to a quantity representative of the load.
: label: EQ-None
textrm {*} frac {{parallel {mathrm {Q}}} ^ {T}mathrm {.} {sigma} _ {i} ^ {n} + {mathrm {B}} ^ {T}mathrm {.} {lambda} _ {i} ^ {n} - {mathrm {L}} - {mathrm {L}}} _ {text {mecha}}parallel}} {{parallel {mathrm {L}} - {mathrm {L}}} - {mathrm {L}}}} {parallel {mathrm {L}}} {{parallel {mathrm {L}}} {{parallel {mathrm {L}}} {parallel {mathrm {L}}} {{parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {parallel {mathrm {L}}} {+ {mathrm {B}}} ^ {T}mathrm {.} {lambda} _ {i} ^ {n}parallel} _ {infty}}leeta
3.4. Dualized boundary conditions — Nonlinear case#
Let us now consider the case of dualized non-linear boundary conditions. For example, LIAISON_SOLIDE in large transformations. It is assumed the existence of a potential \(J(v)\) such that the minimization of the latter makes it possible to express the mechanical balance (in the weak sense) of the structure. If \(J(u)\) is this minimum then we have:
: label: eq-107
begin {array} {c}text {Find} uin Vtext {such as:}\{begin {array} {c} J (u) =underset {vin V} {mathit {min}} {min}}} J (v)} J (v)} J (v)} J (v)} J (v) J (v)} J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v (u, v)}\text {With:} V={vin {R} ^ {n}text {such as}mathit {Bv} =0text {and} C (v) =0} C (v) =0}end {array}end {array}
\({L}^{\text{int}}(u,v)\) refers to the sum of discretized internal forces. It depends on the solution sought via the laws of behavior, the kinematics of large transformations, etc.
\({L}^{\text{ext}}(u,v)\) refers to the sum of discretized external forces. It may depend on the solution as in the case of succeeding forces, contact, etc.
\(V\) refers to all eligible test solutions;
\(U\) refers to all eligible solutions sought;
:math:`B` is a*linear operator of the space of the fields of movements on a space of functions defined on a part of the edge of the structure;
:math:`C(v)` is a*nonlinear operator of the space of the fields of movements on a space of functions defined on a part of the edge of the structure;
As non-linear boundary conditions, we consider the example shown in figure (), we want the solid to remain rigid, i.e. the distance between node \(M\) and the other nodes \({M}_{i}\) to remain constant. That is:
: label: eq-108
C ({u} _ {{M} _ {i}}} - {u} _ {M}) =sqrt {{left ({{x} _ {x}}}}}} _ {{M}}}}} _ {{M} _ {i}}} - {{x}}} - {{x}}} _ {M}}}}} _ {M}}}}} _ {M}}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {M}}}} _ {{left ({{x} _ {vec {{e}} _ {y}}}}}} _ {{M} _ {i}} - {{x} _ {y}}}}}}} _ {M}right)}}} _ {M}right)}}}} _ {M}right)}}}} ^ {2}}} ^ {2}} + {left ({{x} _ {e} _ {z}}}}} _ {M}right)}}} _ {M}right)}}} ^ {2}} + {{x} _ {e} _ {z}}}} {i}} - {{x} _ {vec {{e} _ {z}}}}} _ {M}right)}} ^ {2}}
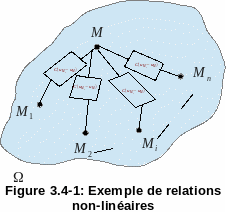
Figure 3.4-1: Example of nonlinear relationships
This relationship is non-linear because it depends on the movements of the various \({M}_{i}\) nodes.
3.4.1. Balance problem under conditions of nonlinear equality#
We assume the existence of a discrete nonlinear equality \(C(u)\) of \({ℝ}^{n}\) in in \(ℝ\) depending on the solution \(\textcolor[rgb]{0,0,0}{u\in {R}^{n}}\) such that we have the following problem:
: label: eq-109
begin {array} {c}text {Find} uin Vtext {such as:}\{begin {array} {c} J (u) =underset {vin V} {mathit {min}} {min}}} J (v)} J (v)} J (v)} J (v)} J (v) J (v)} J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v)} J (v) J (v) J (v (u, v)}\text {With:} V={vin {R} ^ {n}text {such as}mathit {Bv} =0text {and} C (v) =0} C (v) =0}end {array}end {array}
Assume that \(\textcolor[rgb]{0,0,0}{C(\mathrm{.})}\) is a differentiable function [bib3] _ At least of class one. The previous problem () and the problem () are such that we are looking for the minimum in a region of admissible solutions \(\textcolor[rgb]{0,0,0}{V\subset {R}^{n}}\). The difficulty lies in the prior construction of all the admissible solutions, which is not a direct step in the case of the problem () because of the unknown nature (depending on the solution) of this admissible space. We will use the technique of dualization by the Lagrange multipliers, we write the Lagrangian increased by this system:
: label: eq-110
L (v, {lambda}} _ {l} ^ {text {*}}}, {lambda}} _ {mathit {nl}}} ^ {text {*}}) =J (v) + {lambda} _ {l} _ {l} _ {lambda}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}} _ {lambda}} + {mathit {nl}}} ^ {l}} ^ {l}} ^ {l}} ^ {text {*}}} text {*}} C (v)
Hence the following problem equivalent to problem ():
: label: eq-111
begin {array} {c}text {Find the local extremes} uin {riam} ^ {n}, {lambda} _ {l}in riamtext {and} {lambda} _ {lambda} _ {mathit {nl}}} _ {mathit {nl}} _ {lambda}} _ {lambda}} _ {lambda}} _ {lambda}} _ {lambda} _ {lambda}} _ {lambda} _ {lambda}} _ {lambda} _ {lambda}} _ {lambda} _ {lambda}} _ {lambda}} _ {lambda}} _ {lambda}} _ {lambda}} _ {lambda}} _ da} _ {mathit {nl}} ^ {text {*}}})\forall (v, {lambda} _ {l} ^ {text {*}}}, {lambda}} _ {mathit {nl}} _ {mathit {nl}} _ {text {nl}}})\ in {text {*}})in {text {*}})in {text {*}}})in {text {*}})in {text {*}}})in {text {*}})in {text {*}})in {text {*}})in {text {*}})in {text {*}})
To do this, it is sufficient to establish the stationnarity conditions of the Lagrangian, i.e.:
: label: eq-112
{begin {array} {c} {{partial}} _ {partial} _ {v} L (v, {lambda}} _ {text {*}}}, {lambda} _ {mathit {nl}}}}} ^ {mathit {nl}}} ^ {mathit {nl}} ^ {mathit {nl}} ^ {mathit {nl}}} ^ {mathit {nl}}} ^ {text {*}}} ^ {text {*}}} ^ {text {*}}}) {text {*}} L (v, {lambda}}} _ {mathit {nl}}} ^ {mathit {nl}}} ^ {mathit {nl}}} ^ {text {}}}delta v=0\ {{partial} _ {{partial} _ {{lambda}} _ {l}}} L (v, {lambda} _ {l} ^ {text {*}} ^ {text {*}}}, {text {*}}} ^ {text {*}}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text {*}} ^ {text _ {l}, {lambda} _ {mathit {nl}}}}}delta {lambda}} _ {l} ^ {text {*}} =0\ {{partial} _ {{lambda} _ {{lambda}} _ {lambda}} _ {l} _ {l}} _ {l} _ {l} _ {lambda}} _ {l} _ {lambda}} _ {l} _ {lambda}} _ {l} _ {lambda}} _ {l} _ {lambda}} _ {l} _ {lambda}} _ {l}} _ {lambda} _ {lambda}} _ {l}} _ {lambda}} _ {l}} _ {l}}}}, {lambda} _ {mathit {nl}}} ^ {text {*}}})mid} _ {u, {lambda} _ {lambda} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}}} ^ {text {*}} _ {mathit {nl}} _ {mathit {nl}} _ {mathit {nl}}} =0end {array}forall (delta v,delta {lambda}} _ {l}} _ {l}} ^ {text {*}}},delta {lambda}} _ {mathit {nl}}}} ^ {mathit {nl}}} ^ {nl}} ^ {nl}} ^ {nl}}} ^ {mathit {nl}}} ^ {text {*}} ^ {text {*}})in {text {*}}})in {λ} ^ {*}})in {λ} ^ {*}})in {
Hence the following non-linear system to be solved:
That will be written in more compact form:
: label: eq-114
S (u,lambda) =0
3.4.2. Linearization of the problem#
To solve this problem, Newton’s method is also used. But the system must be linearized (). We use time step \({t}_{i}\) (to simplify writing, we omit to specify the dependence of quantities on the time step). We approximate the quantities at the Newton \(n\) iteration, compared to these same quantities at the \(n-1\) iteration:
: label: eq-115
S ({u} ^ {n}, {lambda} ^ {n})approx S ({u} ^ {n-1}, {lambda} ^ {n-1}) +langle {partial} _ {u} _ {u} S ({u} ^ {n}) S ({u} ^ {n}), {lambda} ^ {n-1}),delta urangle +langle {partial} _ {u} _ {u} S ({u} ^ {n-1}),delta urangle +langle {partial} _ {u} _ {u} S ({u} ^ {n}),delta urangle +langle {partial} _ {u} _ {u} S ({u} ^ {n}lambda} S ({u} ^ {n-1}, {lambda} ^ {n-1}),Deltalambdarangleapprox 0
We ask:
: label: eq-116
langle K ({u} ^ {n-1}),Delta un-1}),Delta urangle =langle {partial} _ {u} S ({u} ^ {n-1}, {lambda} ^ {n-1}),Delta urangle +langle +langle {partial} _ {partial} _ {u} S ({u} ^ {n-1}, {lambda} ^ {n-1}), {lambda} ^ {n-1}),Delta urangle +langle {partial} _ {partial} _ {lambda} _ {n-1}, {lambda} ^ {n-1}, {lambda} ^ {n-1}),Delta urangle +langle -1}),Deltalambdarangle
Expanding all the terms:
: label: eq-117
begin {array} {c}langle K ({u} ^ {n-1}),Delta urangle =delta vleft{partial} _ {u} {L} ^ {text {int}, n-1} ^ {text {int}, n-1}, n-1} ^ {text {int}, n-1} ^ {partial}, n-1} ^ {partial} ^ {partial} ^ {2}} _ {{u} ^ {2}}} {mathrm {C}}} ^ {n-1} {lambda} _ {mathit {nl}} ^ {n-1}Delta uright}\ right}\ delta vleft}\delta vleft{delta vleft}}\ left{{delta vleft}} ^ {n-1}left{{mathrm {B}}} ^ {lambda}} ^ {n-1}right} +delta {lambda} _ {l}left{mathrm {B}{mathrm {B}\ delta vleft{{partial} _ {u} {mathrm {C}}} {mathrm {C}}}} ^ {mathrm {C}}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} ^ {mathrm {C}}}} _ {mathit {nl}}left{{partial} _ {u} {mathrm {C}} ^ {n-1}Delta uright}left{{partial}}end {partial} _ {partial} _ {u} {mathrm {C}}} ^ {n-1}Delta uright}right}right
We finally have the following system:
With:
\({K}^{\text{int},n-1}={\partial }_{u}{L}^{\text{int},n-1}\) the classical tangent matrix (see 2.3.2 and 2.4.3);
\(\nabla {\mathrm{C}}^{n-1}={\partial }_{u}{\mathrm{C}}^{n-1}\) the Jacobian matrix of the non-linear relationship;
\(\nabla \nabla {\mathrm{C}}^{n-1}{\lambda }_{\mathit{nl}}^{n-1}={\partial }_{{u}^{2}}^{2}{\mathrm{C}}^{n-1}{\lambda }_{\mathit{nl}}^{n-1}\) the Hessian matrix of the nonlinear relationship
We find the following approximate problem, finding the increments \(\Delta u\in {ℝ}^{n}\), \(\Delta {\lambda }_{l}\in ℝ\) and \(\Delta {\lambda }_{\mathit{nl}}\in ℝ\) of the system in prediction (linearization around the time step \(i\)). In § 2.3.5, we found the expression for the mechanic \(\Delta {L}_{i}^{\text{méca}}\) load increment:
For linear boundary conditions, paragraph § 3.3.1 also gave the expression.
Note the difference between \(\mathrm{B}\), a linear relationship matrix, and \({\mathrm{C}}_{i}\), a non-linear relationship matrix. In fact, the \(\mathrm{B}\) matrix is constant throughout the calculation, while the \({\mathrm{C}}_{i}\) matrix changes with each Newtonian iteration. That’s why the latter is indexed by \(i\), unlike the \(\mathrm{B}\) matrix. Equivalently, during the Newton \(n\) iterations, we need to solve the following system:
: label: eq-121
left [begin {array} {ccc} {K} {K} ^ {text {int, n-1}} + {lambda} _ {mathit {nl}} ^ {n-1}nablanabla {mathrm {C}} ^ {C}} ^ {C}}} ^ {n-1}} ^ {T} & {nabla} ^ {T}} ^ {T} {T} {mathrm}} ^ {T} {mathrm} {C}} ^ {n-1}\mathrm {B} & 0& 0\nabla {mathrm {C}} ^ {n-1} & 0& 0end {array}\ right]right]left\mathrm {B}\ mathrm {B}\ mathrm {B}\ mathrm {B}\ mathrm {B}}\ mathrm {B}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}\ mathrm {B}}{lambda} _ {mathit {nl}}} ^ {n} ^ {n}end {array}right} =left{begin {array} {c} {mathrm {L}}} ^ {text {L}}} ^ {text {L}} ^ {mathrm {L}}} ^ {T}} ^ {T}mathrm {.} {lambda} ^ {n-1}\ {mathrm {u}} ^ {d} -mathrm {B}mathrm {.} {mathrm {u}} ^ {n-1}\ {mathrm {C}}} ^ {n-1} {u} ^ {n-1}end {array}n-1}end {array}right}
Notes:
As in the standard case, it is possible to do some near Newton while ignoring the contribution of \(\nabla \nabla \mathrm{C}\) to the tangent matrix. But it is a choice of the developer because the user does not have access to the choice of updating this term, contrary to the general case;
As the problem becomes non-linear in terms of limit conditions, it is necessary to switch with a matrix updated every Newton iteration (REAC_ITER =1). An alarm message alerts you if you don’t take this step;
3.4.3. Adaptation of the convergence criterion#
It is important to clearly define the stopping criterion at the end of each Newton’s iteration both after the prediction and during the correction. We recall (see § 2.5) that in*Code_Aster, it can be defined in several ways.* Here we explain the adaptation of RESI_GLOB_MAXI and RESI_GLOB_RELA to non-linear cases.
Criterion RESI_GLOB_MAXI is to check that the infinite norm of the residue is less than the \(\gamma\) value specified by the user. It is necessary to introduce the contribution of non-linear boundary conditions:
: label: eq-122
{parallel {mathrm {Q}}} ^ {T}mathrm {.} {sigma} _ {i} ^ {n} + {mathrm {B}} ^ {T}mathrm {.} {lambda} _ {i} ^ {n} + {nabla {mathrm {C}} _ {i}} ^ {n, T}mathrm {.} {lambda} _ {mathit {nl}, i}} ^ {n} - {mathrm {L}} _ {i} ^ {text {mecha}}parallel}}parallel} _ {infty} _ {infty}legamma
Criterion RESI_GLOB_RELA (chosen by default) amounts to verifying that the residue is sufficiently small, as before, and this in relation to a quantity representative of the load.