1. Introduction

The HHO methods have been developed over the last few years by Di Pietro, Ern and their collaborators. Early work focuses on the problems of linear diffusion [2] and linear elasticity [3]. Since then, HHO methods have been extended to different physics to deal with such linear problems. only non-linear (see [1] for the references that follow). A complete introduction and application review is given in [9] For linear problems, we can cite work on the Stokes problem, on linear diffusion with variable coefficients, on advection-diffusion-reaction, on the Cahn-Hilliard problem, and on flows in fractured porous media. The use of curved meshes is considered for the problem of linear diffusion. For non-linear problems, we can cite work on the Leray-Lions problem, on stationary Navier-Stokes equations, on spectral problems, and on Bingham fluids. With particular reference to solid mechanics, there has been an extension to the problem of non-linear elasticity. in small deformations, to the Biot problem, to the equations of the Kirchhoff–Love plates, and the work carried out in [1] on hyperelasticity in large deformations [4], plasticity in small [5] and large [6] deformations and unilateral contact with Tresca friction. From a numerical point of view, particular interest has been paid to the implementation of these methods in a generic way. so as to include polyhedral meshes of any size.

Methods HHO are non-compliant methods like discontinuous Galerkin (dG) methods, but unlike the latter, they are formulated in terms of unknowns of faces (carried by the skeleton of the mesh). Unknowns in the cells are also added for stability and approximation properties (hence the term Hybrid). These cell unknowns can be eliminated locally by static condensation (or Schur complement). The term High-Order comes from the fact that HHO methods allow you to do both low and high order. without changing the method. The construction of the HHO methods is based on two ideas:

1. the local reconstruction of a gradient or a potential based on the unknowns of the cell and the unknowns of the faces by « mimicking » integration by parts;

2. a local stabilization operator in order to weakly impose on each face of the cell the consistency between the unknowns of the face and the trace of the unknowns of the cell.

The HHO methods have a number of advantages:

1. arbitrary approximation order (\(k \geq 0\) for linear diffusion and \(k \geq 1\) for linear elasticity);

2. use of polyhedral meshes with possibly non-compliant interfaces (see for examples of maillages polyédriques);

3. robustness with respect to physical parameters (elastic incompressibility, dominant advection…) );

4. attractive numerical costs thanks to static condensation that eliminates the unknowns carried by the cells while maintaining a compact stencil;

5. local conservation of flows on each face of the mesh.

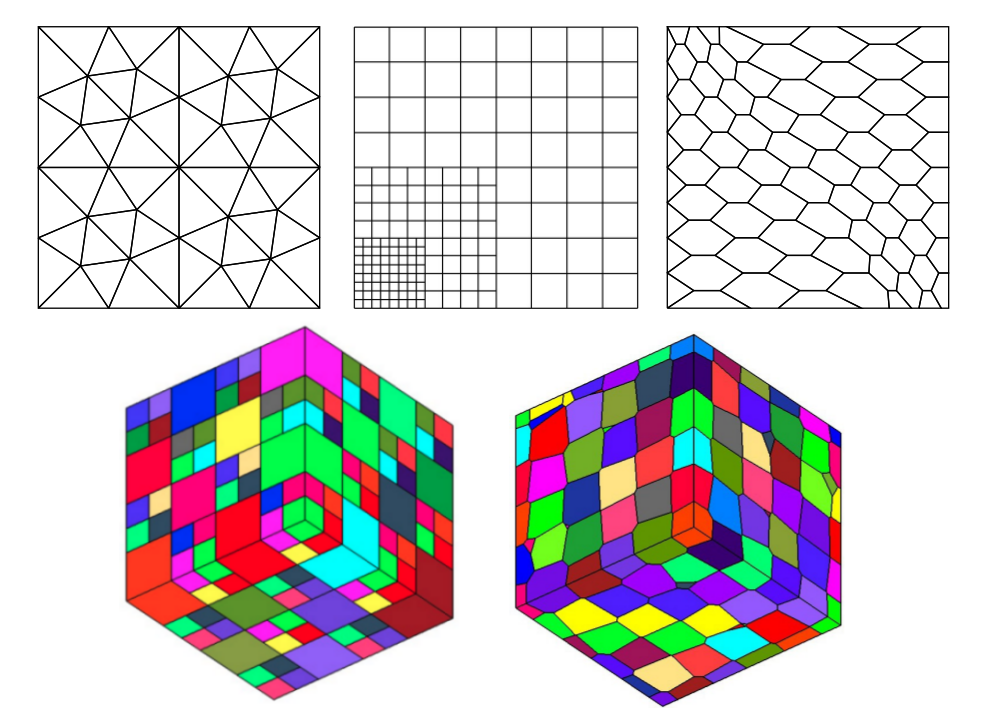
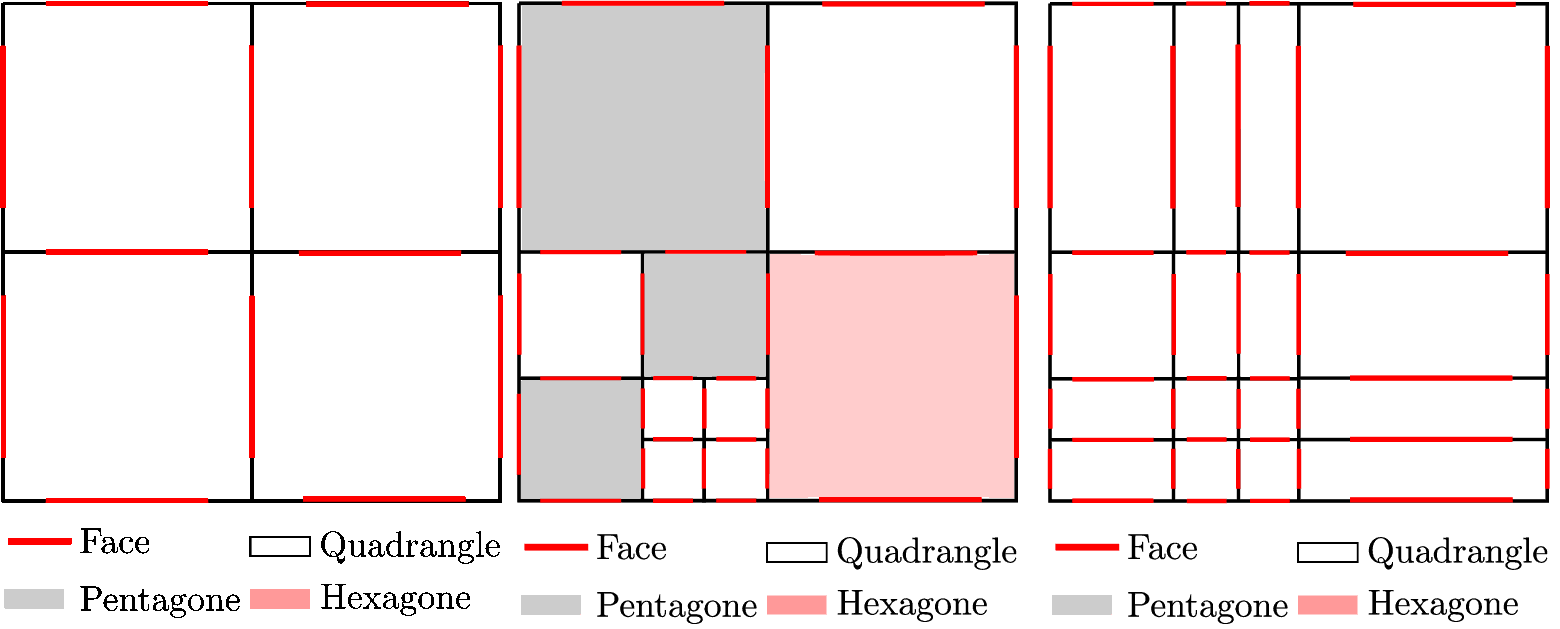
The point (3) is particularly relevant in the context of this manuscript, where we are interested in problems solid mechanics because methods HHO will allow us to use a purely primal formulation (without adding Lagrange multipliers unlike mixed formulations) in order to eliminate digital locking resulting from the incompressibility that is usually present for \(H^1\) -compliant methods. As for the point (2), one motivation is to be able to achieve a local refinement of the mesh without having to worry about the possible presence of orphan nodes as in the \(H^1\) -compliant methods. Indeed, as illustrated in this figure, the presence of orphan nodes is managed simply by treating the corresponding cell as a polygon (or a polyhedron).

The HHO methods have more or less close connections with other numerical methods developed in recent years. For low-order methods, there are links with the Hybrid Finite Volumes and Mixed Finite Volumes finite volume methods, with the Mimetic Finite Differences methods (see [8] for a unified framework of the three previous methods), as well as with Compatible Discrete Operator methods and Gradient Schemes. For higher order methods, a connection has been established between methods HHO, Hybridizable Discontinuous Galerkin (HDG) and Nonconforming Virtual Element Methods (nc VEM). The main similarities and differences between the HHO, HDG, and nc VEM methods are:

• the reconstruction of the discrete operators for HHO replaces the flow equations for HDG and these operators play the same role as the projection operators used by nc VEM;

• the stabilization operators for HHO and HDG are defined from a functional point of view (and are different in the case where the cell unknowns have the same degree as the face unknowns) whereas for nc VEM, these operators are defined from an algebraic point of view while leading to quadratic forms equivalent to HHO.