3. Implementation#
Implementing new numerical methods in code_aster that differ from Lagrange elements can be difficult. We list the main reasons:
Limited number of geometric supports possible in the mesh: triangle and quadrangle in 2D, and tetrahedron, hexahedron, prism and pyramid in 3D (no support for polyhedral meshes);
Strong connection between the geometric support and the selected element. The degree of approximation of the method is determined by the geometric support. For example, a linear approximation for triangles with 3 knots (TRIA3) and quadratic approximation for triangles with 6 nodes (TRIA6);
Finite element unknowns are supported only by physical nodes in the mesh (and not by mesh faces or cells as is the case for finite volume, discontinuous Galerkin, and HHO methods).
The main objective for implementing HHO methods in code_aster is to reuse the code architecture as much as possible and not to change the critical points of the code, which are:
Data structures
Finite element catalogs
The location of the elementary calculations
The assembly operation
We limit ourselves to implementing the HHO methods in code_aster to existing geometric supports. In addition, only linear \(k=1\) and quadratic \(k=2\) approximations are implemented. The various modifications are limited to two operators:
CREA_MAILLAGE: option MODI_HHO
DEFI_MATERIAU: option HHO
3.1. Unknowns HHO and numbering#
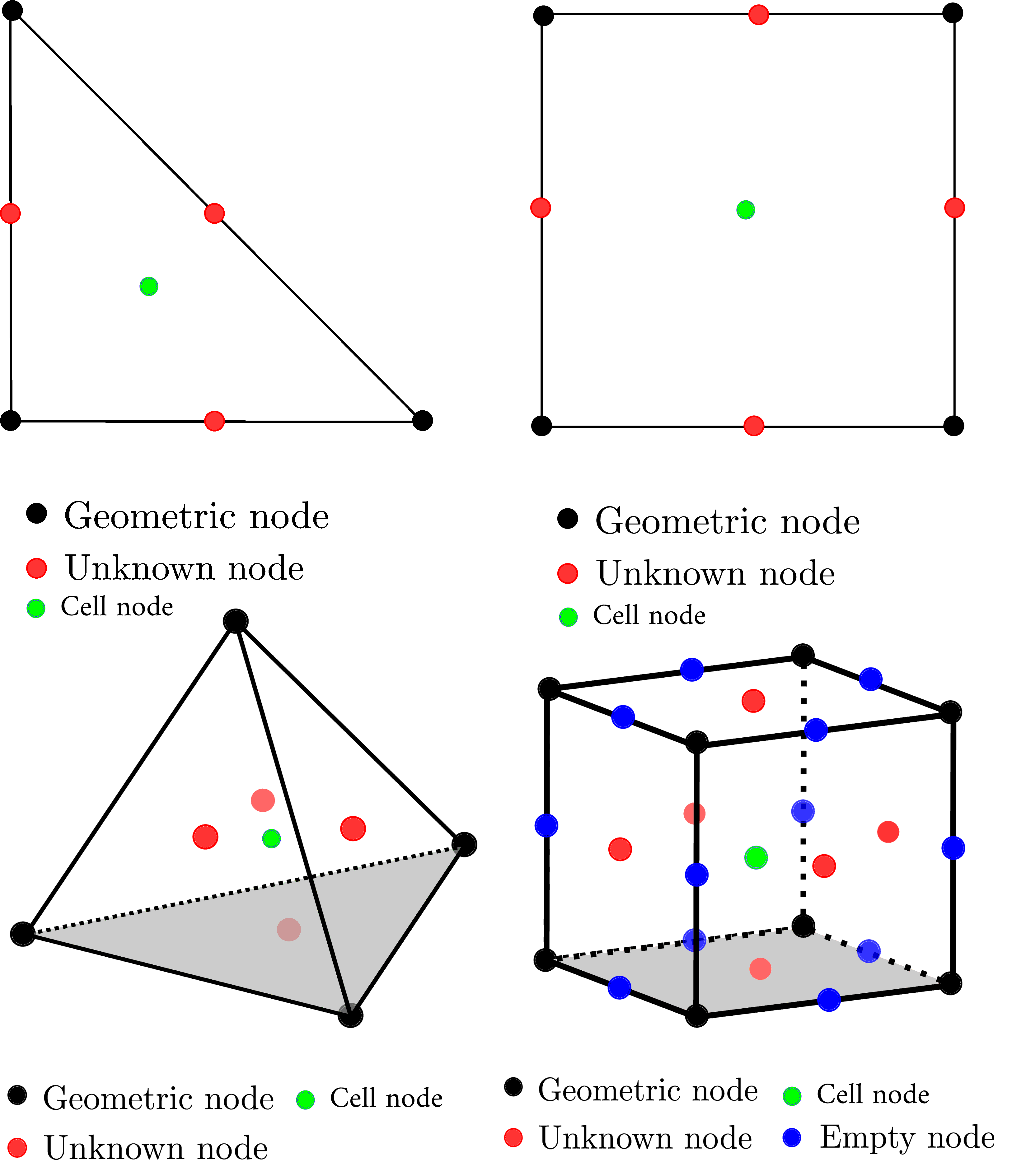
We recall that the unknowns HHO, \({\widehat{v}}_{T}=({v}_{T},{v}_{\partial T})\in {U}_{T}^{k}\), that we calculate are the coefficients of the polynomials of the cells and the faces (these coefficients have no physical meaning in principle). Because, the assembly must be done face by face (and cell by cell) and the unknowns HHO cannot be supported that by physical nodes in the mesh in*code_aster*, we need each mesh face to have at least one node that is not shared with any other face of the mesh (typically a node located at the barycenter of the face) and that it There is a node at the barycenter of the cell. This is the case in 2D for the 7-node triangle (TRIA7) and the 9-node quadrangle (QUAD9), and in 3D for the 27-node hexahedron (HEXA27). These geometric supports correspond to the quadratic elements for the isoparametric elements. Unfortunately, there are no tetrahedra, prisms, and pyramids with this property in code_aster. That’s why we added a mesh converter in CREA_MAILLAGE called MODI_HHO which makes it possible to transform a 4-node tetrahedron into a 15-node tetrahedron (the same goes for prisms (PENTA21) and pyramids (PYRAM19)). The new nodes are located at the barycenter of the faces and the cell.
Face \({v}_{F}\) unknowns for \(F\in {F}_{h}\) faces are supported by the node which is located at the barycenter of face \(F\). These physical mesh nodes that support face unknowns are named unknown_nodes. In addition, as faces are assumed to be flat, we use vertex nodes to describe the geometry of cells and faces; and to calculate the various integrals. These physical mesh nodes that describe geometry are named*geometric_nodes*. Finally, the nodes located in the middle of the segments are not used and are named empty_nodes. These different types of knots are shown ici. These tips on locating unknowns HHO allow data structures and assembly to be reused without changes.
Note (Static Condensation):
*Static condensation (or Schur complement) makes it possible to locally eliminate cell unknowns in elementary contributions (at the end, a smaller problem consisting only of the face unknowns is solved). One of the main difficulties is that the elementary contributions are calculated locally to the element (cell or face) then assembled directly into the global problem using numbering. Whereas for methods HHO, static condensation must be performed prior to assembly to eliminate cell unknowns. For reasons of simplicity, static condensation is not implemented in order not to change the architecture of the code. *
3.2. Dirichlet boundary conditions#
Dirichlet boundary conditions are strongly imposed by modifying the matrix and the load. The user must specify the movements imposed on the edge of Dirichlet. However, it is not easy for the user to give the values of the unknowns of faces and cells because these coefficients a prima facie have no physical meaning. We added an automatic translator that calculates the projection \(L^2\), \({\Pi }_{F}^{k}({u}_{D})\), and imposes the value \({v}_{F}={\Pi}_{F}^{k}({u}_{D})\) from the given displacement \({u}_{D}\) on the nodes of the face (in the continuous sense). In practice, in AFFE_CHAR_CINE, all you have to do is give the conditions on DX, DY and/or DZ and the operator automatically translates it into conditions on polynomials HHO.
3.3. Post-treatment#
Unknowns HHO are polynomial coefficients. In principle, these coefficients have no physical meaning. Thus, post-treatment must be applied in order to be able to visualize these results. We are creating a new field NOEU which will interpolate, in the sense of the Lagrange elements, the unknowns HHO in the field HHO_DEPL. at the end of the calculation. The value of the displacement in a node in the mesh is the average of the values of the unknowns of the cell that contains this node. Note that this field is continuous unlike fields HHO. It should be noted that this field is not in balance with that of constraints. It is there for purely visual purposes. The same post-processing is applied to the speed and acceleration fields in the dynamic case.
3.4. Scope of use#
Method HHO can only be used in static and transient nonlinear mechanics (STAT_NON_LINE/DYNA_NON_LINE) and in linear and non-linear thermics (THER_LINEAIRE/THER_NON_LINE)
The following features are excluded:
touch/friction
piloting
model reduction
macro-elements
calculation of vibration modes or buckling criteria
The method can be used for laws of behavior in small and large deformations (model GDEF_LOG, PETIT, GREEN_LAGRANGE).
Furthermore, the HHO method cannot be used simultaneously with a standard finite element method. Boundary conditions can only be affected by elimination (AFFE_CHAR_CINE (_F)).
Most volume and surface loads are available.
The method works on all 2D and 3D elements of the code. You may need to use CREA_MAILLAGE/MODI_HHO for make the mesh compatible.
Some parameters such as the stabilization coefficient can be defined by zone in DEFI_MATERIAU/HHO. If no value is given an automatic value is calculated from the elastic parameters.