4. Volumic elements

4.1. Tetrahedra: ELREFE TE4, T10

Node coordinates:

	\(x\)	\(y\)	\(z\)
\(\mathrm{N1}\)
\(\mathrm{N2}\)
\(\mathrm{N3}\)
\(\mathrm{N4}\)
\(\mathrm{N5}\)		0.5	0.5
\(\mathrm{N6}\)			0.5
\(\mathrm{N7}\)		0.5
\(\mathrm{N8}\)	0.5	0.5	0.5
\(\mathrm{N9}\)	0.5		0.5
\(\mathrm{N10}\)	0.5

Shape functions:

4-knot formula

\(\{\begin{array}{}{w}_{1}(x,y,z)=y\\ {w}_{2}(x,y,z)=z\\ {w}_{3}(x,y,z)=1-x-y-z\\ {w}_{4}(x,y,z)=x\end{array}\)

10-knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=y(2y-1)\\ {w}_{2}=z(2z-1)\\ {w}_{3}=(1-x-y-z)(1-2x-2y-2z)\\ {w}_{4}=x(2x-1)\\ {w}_{5}=4yz\end{array}\end{split}\]

Numerical integration formula:

Formula with 1 point, order 1 in \(x,y,z\): (FPG1)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(1/4\)	\(1/4\)		\(1/4\)	\(1/6\)

Formula with 4 points, order 2 in \(x,y,z\): (FPG4)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(a\)	\(a\)		\(a\)	\(1/24\)
2	\(a\)	\(a\)		\(b\)	\(1/24\)
3	\(a\)	\(b\)		\(a\)	\(1/24\)
4	\(b\)	\(a\)		\(a\)	\(1/24\)

with: \(a=\frac{5-\sqrt{5}}{\text{20}}\), \(b=\frac{5+3\sqrt{5}}{\text{20}}\)

Formula with 5 points, order 3 in \(x,y,z\): (FPG5)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(a\)	\(a\)		\(a\)	\(-2/15\)
2	\(b\)	\(b\)		\(b\)	\(3/40\)
3	\(b\)	\(b\)		\(c\)	\(3/40\)
4	\(b\)	\(c\)		\(b\)	\(3/40\)
5	\(c\)	\(b\)		\(b\)	\(3/40\)

With: \(a=0\text{.}\text{25}\), \(b=\frac{1}{6}\), \(c=0\text{.}5\)

Formula with 15 points, order 5 in \(x,y,z\): (FPG15)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(a\)	\(a\)		\(a\)	\(8/405\)
2 3 4 5	\({b}_{1}\) \({b}_{1}\) \({b}_{1}\) \({c}_{1}\)	\({b}_{1}\) \({b}_{1}\) \({c}_{1}\) \({b}_{1}\)	\({b}_{1}\) \({c}_{1}\) \({b}_{1}\) \({b}_{1}\)	\(\frac{2\text{665}-\text{14}\sqrt{\text{15}}}{\text{226}\text{800}}\)
6 7 8 9	\({b}_{2}\) \({b}_{2}\) \({b}_{2}\) \({c}_{2}\)	\({b}_{2}\) \({b}_{2}\) \({c}_{2}\) \({b}_{2}\)	\({b}_{2}\) \({c}_{2}\) \({b}_{2}\) \({b}_{2}\)	\(\frac{2\text{665}+\text{14}\sqrt{\text{15}}}{\text{226}\text{800}}\)
10 11 12 13 14 15	\(d\) \(d\) \(e\) \(d\) \(e\) \(e\)	\(d\) \(e\) \(d\) \(e\) \(d\) \(e\)	\(e\) \(d\) \(d\) \(e\) \(e\) \(d\)	\(\frac{5}{\text{567}}\)

with:

\(a=0\text{.}\text{25}\)

\(\begin{array}{}{b}_{1}=\frac{7+\sqrt{\text{15}}}{\text{34}}\\ {b}_{2}=\frac{7-\sqrt{\text{15}}}{\text{34}}\end{array}\)

\(\begin{array}{}{c}_{1}=\frac{\text{13}-3\sqrt{\text{15}}}{\text{34}}\\ {c}_{2}=\frac{\text{13}+3\sqrt{\text{15}}}{\text{34}}\end{array}\)

\(\begin{array}{}d=\frac{5-\sqrt{\text{15}}}{\text{20}}\\ e=\frac{5+\sqrt{\text{15}}}{\text{20}}\end{array}\)

4.2. Pentahedra: ELREFE PE6, P15, P15, P18, P21

N19 ROAD

N20 ROAD

N21 ROAD

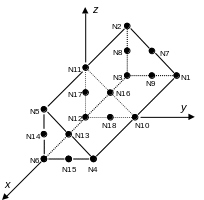
Node coordinates:

	\(x\)	\(y\)	\(z\)
\(\mathrm{N1}\)	-1.
\(\mathrm{N2}\)	-1.
\(\mathrm{N3}\)	-1.
\(\mathrm{N4}\)
\(\mathrm{N5}\)
\(\mathrm{N6}\)
\(\mathrm{N7}\)	-1.	0.5	0.5.
\(\mathrm{N8}\)	-1.		0.5.
\(\mathrm{N9}\)	-1.	0.5
\(\mathrm{N10}\)
\(\mathrm{N11}\)
\(\mathrm{N12}\)
\(\mathrm{N13}\)		0.5	0.5
\(\mathrm{N14}\)			0.5
\(\mathrm{N15}\)		0.5
\(\mathrm{N16}\)		0.5	0.5
\(N17\)			0.5
\(\mathrm{N18}\)		0.5
\(N19\)	-1.	1/3	1/3
\(N20\)		1/3	1/3
\(N21\)		1/3	1/3

Shape functions:

6-knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=\frac{1}{2}y(1-x)\\ {w}_{2}=\frac{1}{2}z(1-x)\\ {w}_{3}=\frac{1}{2}(1-y-z)(1-x)\end{array}\end{split}\]

15-knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=y(1-x)(2y-2-x)/2\\ {w}_{2}=z(1-x)(2z-2-x)/2\\ {w}_{3}=(x-1)(1-y-z)(x+2y+2z)/2\\ {w}_{4}=y(1+x)(2y-2+x)/2\\ {w}_{5}=z(1+x)(2z-2+x)/2\\ {w}_{6}=(-x-1)(1-y-z)(-x+2y+2z)/2\\ {w}_{7}=2yz(1-x)\\ {w}_{8}=2z(1-y-z)(1-x)\end{array}\end{split}\]

18 knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=xy(x-1)(2y-1)/2\\ {w}_{2}=xz(x-1)(2z-1)/2\\ {w}_{3}=x(x-1)(z+y-1)(2z+2y-1)/2\\ {w}_{4}=xy(x+1)(2y-1)/2\\ {w}_{5}=xz(x+1)(2z-1)/2\\ {w}_{6}=x(x+1)(z+y-1)(2z+2y-1)/2\\ {w}_{7}=2xyz(x-1)\\ {w}_{8}=-2xz(x-1)(z+y-1)\\ {w}_{9}=-2xy(x-1)(z+y-1)\end{array}\end{split}\]

6-point numerical integration formulas (order 3 in \(x\), order 2 in \(y\) and \(z\)) (FPG6)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(-1/\sqrt{3}\)	0.5	0.5	\(1/6\)
2	\(-1/\sqrt{3}\)		0.5	\(1/6\)
3	\(-1/\sqrt{3}\)	0.5		\(1/6\)
4	\(1/\sqrt{3}\)	0.5	0.5	\(1/6\)
5	\(1/\sqrt{3}\)		0.5	\(1/6\)
6	\(1/\sqrt{3}\)	0.5		\(1/6\)

8-point numerical integration formula: (FPG8)

2 Gauss points in \(x\) (order 3).

4 Hammer points in \(y\) and \(z\) (3rd order).

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(-a\)	\(1/3\)		\(1/3\)	\(-27/96\)
2	\(-a\)	0.6	0.2	\(25/96\)
3	\(-a\)	0.2	0.6	\(25/96\)
4	\(-a\)	0.2	0.2	\(25/96\)
5	\(+a\)	\(1/3\)		\(1/3\)	\(-27/96\)
6	\(+a\)	0.6	0.2	\(25/96\)
7	\(+a\)	0.2	0.6	\(25/96\)
8	\(+a\)	0.2	0.2	\(25/96\)

With \(a=0.577350269189626\)

21-point numerical integration formula: (FPG21)

3 Gauss points in \(x\) (order 5).

7 Hammer points in \(y\) and \(z\) (order 5 in \(y\) and \(z\)).

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(-\alpha\)	\(1/3\)		\(1/3\)	\({c}_{1}\frac{9}{80}\)
2 3 4	\(-\alpha\) \(-\alpha\) \(-\alpha\)	\(a\) \(1-\mathrm{2a}\) \(a\)	\(a\) \(a\) \(1-\mathrm{2a}\)	\({c}_{1}(\frac{155+\sqrt{15}}{2400})\)
5 6 7	\(-\alpha\) \(-\alpha\) \(-\alpha\)	\(b\) \(1-\mathrm{2b}\) \(b\)	\(b\) \(b\) \(1-\mathrm{2b}\)	\({c}_{1}(\frac{155-\sqrt{15}}{2400})\)
8		\(1/3\)	\(1/3\)	\({c}_{2}\frac{9}{80}\)
9 10 11	0. 0. 0.	\(a\) \(1-\mathrm{2a}\) \(a\)	\(a\) \(a\) \(1-\mathrm{2a}\)	\({c}_{2}(\frac{155+\sqrt{15}}{2400})\)
12 13 14	0. 0. 0.	\(b\) \(1-\mathrm{2b}\) \(b\)	\(b\) \(b\) \(1-\mathrm{2b}\)	\({c}_{2}(\frac{155-\sqrt{15}}{2400})\)
15	\(\alpha\)	\(1/3\)		\(1/3\)	\({c}_{1}\frac{9}{80}\)
16 17 18	\(\alpha\) \(\alpha\) \(\alpha\)	\(b\) \(1-\mathrm{2a}\) \(a\)	\(a\) \(a\) \(1-\mathrm{2a}\)	\({c}_{1}(\frac{155+\sqrt{15}}{2400})\)
19 20 21	\(\alpha\) \(\alpha\) \(\alpha\)	\(b\) \(1-\mathrm{2b}\) \(b\)	\(b\) \(b\) \(1-\mathrm{2b}\)	\({c}_{1}(\frac{155-\sqrt{15}}{2400})\)

with:

\(\alpha =\sqrt{\frac{3}{5}}\)

\({c}_{1}=\frac{5}{9}\)

\({c}_{2}=\frac{8}{9}\)

\(a=\frac{6+\sqrt{15}}{21}\)

\(b=\frac{6-\sqrt{15}}{21}\)

27-point numerical integration formula (FPG27): see [bib3].

Point	\(x\)	\(y\)		\(z\)	Weight
1	0.0	0.895512822481133	0.052243588759434	0.027191062410231
2	0.0	0.052243588759434	0.052243588759434	0.895512822481133	0.027191062410231
3	0.0	0.052243588759434	0.052243588759434	0.027191062410231
4	0.0	0.198304865473555	0.270635256143164	0.040636041641641220
5	0.0	0.198304865473555	0.531059878383280	0.040636041641641220
6	0.0	0.270635256143164	0.531059878383280	0.040636041641641220
7	0.0	0.531059878383280	0.270635256143164	0.040636041641641220
8	0.0	0.531059878383280	0.198304865473555	0.040636041641641220
9	0.0	0.270635256143164	0.198304865473555	0.040636041641641220
10	0.936241512371697	0.3333333333333333333	0.33333333333333333	0.05027512371697	0.050275140937507
11	0.948681147283254	0.841699897299232	0.079150051350384	0.011774414962347
12	0.948681147283254	0.079150051350384	0.841699897299232	0.011774414962347
13	0.948681147283254	0.079150051350384	0.079150051350384	0.011774414962347
14	0.600638052820557	0.054831294873304	0.308513201856883	0.041951149272741
15	0.600638052820557	0.054831294873304	0.636655503269814	0.041951149272741
16	0.600638052820557	0.308513201856883	0.636655503269814	0.041951149272741
17	0.600638052820557	0.636655503269814	0.308513201856883	0.041951149272741
18	0.600638052820557	0.636655503269814	0.054831294873304	0.041951149272741
19	0.600638052820557	0.308513201856883	0.054831294873304	0.041951149272741
20	-0.93624151212371697	0.3333333333333333333	0.33333333333333333	0.05027512371697	0.050275140937507
21	-0.948681147283254	0.841699897299232	0.079150051350384	0.011774414962347
22	-0.948681147283254	0.079150051350384	0.841699897299232	0.011774414962347
23	-0.948681147283254	0.079150051350384	0.079150051350384	0.011774414962347
24	-0.600638052820557	0.054831294873304	0.308513201856883	0.041951149272741
25	-0.600638052820557	0.054831294873304	0.636655503269814	0.0419511492820557	0.041951149272741
26	-0.600638052820557	0.308513201856883	0.636655503269814	0.0419511492820557	0.041951149272741
27	-0.600638052820557	0.636655503269814	0.308513201856883	0.041951149272741
28	-0.600638052820557	0.636655503269814	0.054831294873304	0.041951149272741
29	-0.600638052820557	0.308513201856883	0.054831294873304	0.041951149272741

4.3. Hexahedra: ELREFE HE8, H20, H27

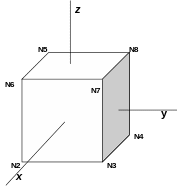
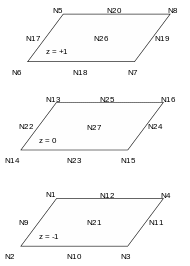
Node coordinates:

	\(x\)	\(y\)	\(z\)
N1	-1.	-1.	-1.
N2		-1.	-1.
N3			-1.
N4	-1.		-1.
N5	-1.	-1.
N6		-1.
N7
N8	-1.
N9		-1.	-1.
N10			-1.
N11			-1.
N12	-1.		-1.
N13	-1.	-1.
N14		-1.
N15
N16	-1.
N17		-1.
N18
N19
N20	-1.
N21			-1.
N22		-1.
N23
N24
N25	-1.
N26
N27

Shape functions:

8-knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=\frac{1}{8}(1-x)(1-y)(1-z)\\ {w}_{2}=\frac{1}{8}(1+x)(1-y)(1-z)\\ {w}_{3}=\frac{1}{8}(1+x)(1+y)(1-z)\\ {w}_{4}=\frac{1}{8}(1-x)(1+y)(1-z)\end{array}\end{split}\]

20-knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=\frac{1}{8}(1-x)(1-y)(1-z)(-2-x-y-z)\\ {w}_{2}=\frac{1}{8}(1+x)(1-y)(1-z)(-2+x-y-z)\\ {w}_{3}=\frac{1}{8}(1+x)(1+y)(1-z)(-2+x+y-z)\\ {w}_{4}=\frac{1}{8}(1-x)(1+y)(1-z)(-2-x+y-z)\\ {w}_{5}=\frac{1}{8}(1-x)(1-y)(1+z)(-2-x-y+z)\\ {w}_{6}=\frac{1}{8}(1+x)(1-y)(1+z)(-2+x-y+z)\\ {w}_{7}=\frac{1}{8}(1+x)(1+y)(1+z)(-2+x+y+z)\\ {w}_{8}=\frac{1}{8}(1-x)(1+y)(1+z)(-2-x+y+z)\\ {w}_{9}=\frac{1}{4}(1-{x}^{2})(1-y)(1-z)\\ {w}_{10}=\frac{1}{4}(1-{y}^{2})(1+x)(1-z)\end{array}\end{split}\]

27-knot formula

(4.7)\[\begin{split}\begin{array}{}{w}_{1}=\frac{1}{8}x(x-1)y(y-1)z(z-1)\\ {w}_{2}=\frac{1}{8}x(x+1)y(y-1)z(z-1)\\ {w}_{3}=\frac{1}{8}x(x+1)y(y+1)z(z-1)\\ {w}_{4}=\frac{1}{8}x(x-1)y(y+1)z(z-1)\\ {w}_{5}=\frac{1}{8}x(x-1)y(y-1)z(z+1)\\ {w}_{6}=\frac{1}{8}x(x+1)y(y-1)z(z+1)\\ {w}_{7}=\frac{1}{8}x(x+1)y(y+1)z(z+1)\\ {w}_{8}=\frac{1}{8}x(x-1)y(y+1)z(z+1)\\ {w}_{9}=\frac{1}{4}(1-{x}^{2})y(y-1)z(z-1)\\ {w}_{\text{10}}=\frac{1}{4}x(x+1)(1-{y}^{2})z(z-1)\\ {w}_{\text{11}}=\frac{1}{4}(1-{x}^{2})y(y+1)z(z-1)\\ {w}_{\text{12}}=\frac{1}{4}x(x-1)(1-{y}^{2})z(z-1)\\ {w}_{\text{13}}=\frac{1}{4}x(x-1)y(y-1)(1-{z}^{2})\\ {w}_{\text{14}}=\frac{1}{4}x(x+1)y(y-1)(1-{z}^{2})\end{array}\end{split}\]

Gauss quadrature formula with 2 points in each direction (order 3) (FPG8)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(-1/\sqrt{3}\)	\(-1/\sqrt{3}\)		\(-1/\sqrt{3}\)
2	\(-1/\sqrt{3}\)	\(-1/\sqrt{3}\)		\(1/\sqrt{3}\)
3	\(-1/\sqrt{3}\)	\(1/\sqrt{3}\)		\(-1/\sqrt{3}\)
4	\(-1/\sqrt{3}\)	\(1/\sqrt{3}\)		\(1/\sqrt{3}\)
5	\(1/\sqrt{3}\)	\(-1/\sqrt{3}\)		\(-1/\sqrt{3}\)
6	\(1/\sqrt{3}\)	\(-1/\sqrt{3}\)		\(1/\sqrt{3}\)
7	\(1/\sqrt{3}\)	\(1/\sqrt{3}\)		\(-1/\sqrt{3}\)
8	\(1/\sqrt{3}\)	\(1/\sqrt{3}\)		\(1/\sqrt{3}\)

Gauss quadrature formula with 3 points in each direction (order 5): (FPG27)

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(-\alpha\)	\(-\alpha\)		\(-\alpha\)	\({c}_{1}^{3}\)
2	\(-\alpha\)	\(-\alpha\)		\({c}_{1}^{2}{c}_{2}\)
3	\(-\alpha\)	\(-\alpha\)		\(\alpha\)	\({c}_{1}^{3}\)
4	\(-\alpha\)		\(-\alpha\)	\({c}_{1}^{2}{c}_{2}\)
5	\(-\alpha\)			\({c}_{1}{c}_{2}^{2}\)
6	\(-\alpha\)		\(\alpha\)	\({c}_{1}^{2}{c}_{2}\)
7	\(-\alpha\)	\(\alpha\)		\(-\alpha\)	\({c}_{1}^{3}\)
8	\(-\alpha\)	\(\alpha\)		\({c}_{1}^{2}{c}_{2}\)
9	\(-\alpha\)	\(\alpha\)		\(\alpha\)	\({c}_{1}^{3}\)
10		\(-\alpha\)	\(-\alpha\)	\({c}_{1}^{2}{c}_{2}\)
11		\(-\alpha\)		\({c}_{1}{c}_{2}^{2}\)
12		\(-\alpha\)	\(\alpha\)	\({c}_{1}^{2}{c}_{2}\)
13			\(-\alpha\)	\({c}_{1}{c}_{2}^{2}\)
14				\({c}_{2}^{3}\)
15			\(\alpha\)	\({c}_{1}{c}_{2}^{2}\)
16		\(\alpha\)	\(-\alpha\)	\({c}_{1}^{2}{c}_{2}\)
17		\(\alpha\)		\({c}_{1}{c}_{2}^{2}\)
18		\(\alpha\)	\(\alpha\)	\({c}_{1}^{2}{c}_{2}\)
19	\(\alpha\)	\(-\alpha\)		\(-\alpha\)	\({c}_{1}^{3}\)
20	\(\alpha\)	\(-\alpha\)		\({c}_{1}^{2}{c}_{2}\)
21	\(\alpha\)	\(-\alpha\)		\(\alpha\)	\({c}_{1}^{3}\)
22	\(\alpha\)		\(-\alpha\)	\({c}_{1}^{2}{c}_{2}\)
23	\(\alpha\)			\({c}_{1}{c}_{2}^{2}\)
24	\(\alpha\)		\(\alpha\)	\({c}_{1}^{2}{c}_{2}\)
25	\(\alpha\)	\(\alpha\)		\(-\alpha\)	\({c}_{1}^{3}\)
26	\(\alpha\)	\(\alpha\)		\({c}_{1}^{2}{c}_{2}\)
27	\(\alpha\)	\(\alpha\)		\(\alpha\)	\({c}_{1}^{3}\)

with:

\(\alpha =\sqrt{\frac{3}{5}}\)

\({c}_{1}=\frac{5}{9}\)

\({c}_{2}=\frac{8}{9}\)

4.4. Pyramids: ELREFE PY5, P13, P19

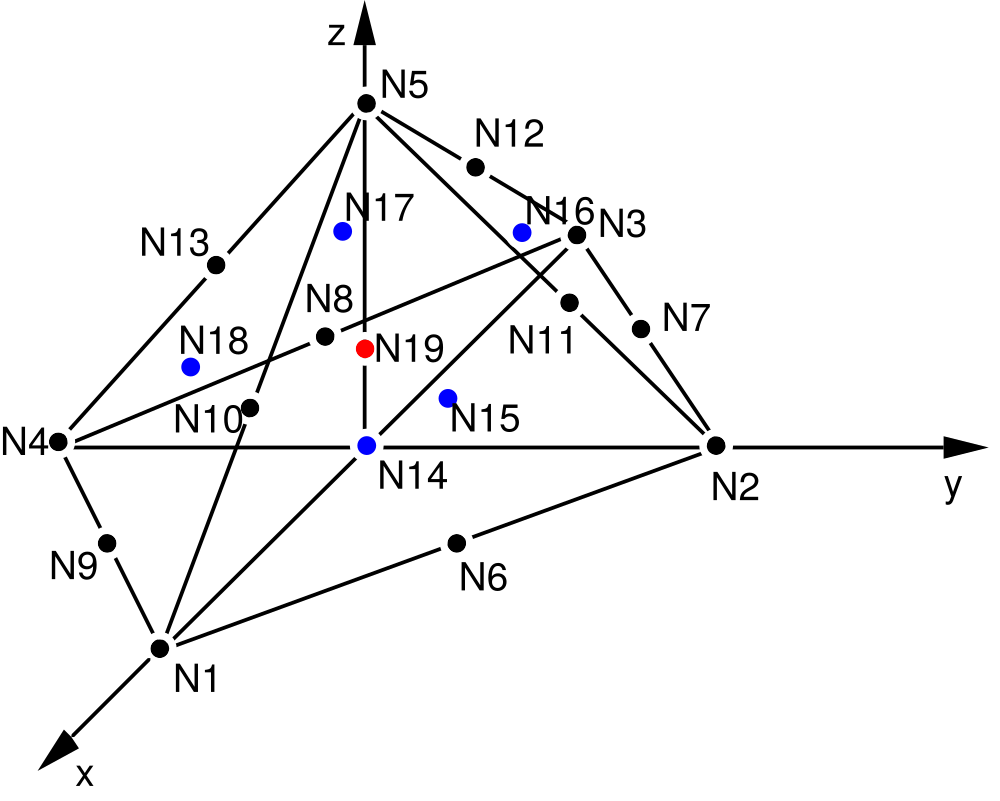
The blue nodes are in the middle of the faces, the red one is in the middle of the cell.

The square base is made up of the quadrangle \({N}_{1}{N}_{2}{N}_{3}{N}_{4}\) and \({N}_{5}\) is the top of the pyramid.

	\(x\)	\(y\)	\(z\)
\({N}_{1}\)
\({N}_{2}\)
\({N}_{3}\)	—1.
\({N}_{4}\)		—1.
\({N}_{5}\)
\({N}_{6}\)	0.5	0.5	0.5
\({N}_{7}\)	—0.5	0.5
\({N}_{8}\)	—0.5	—0.5
\({N}_{9}\)	0.5	—0.5
\({N}_{10}\)	0.5		0.5
\({N}_{11}\)		0.5	0.5
\({N}_{12}\)	—0.5		0.5
\({N}_{13}\)		—0.5	0.5
\({N}_{14}\)			0
\({N}_{15}\)	1/3	1/3	1/3
\({N}_{16}\)	-1/3	1/3	1/3
\({N}_{17}\)	-1/3	-1/3	1/3
\({N}_{18}\)	1/3	-1/3	1/3
\({N}_{19}\)	0	0	0	0.2

Shape functions:

5-knot formula

\(\begin{array}{}{w}_{1}=\frac{(-x+y+z-1)(-x-y+z-1)}{4(1-z)}\\ {w}_{2}=\frac{(-x-y+z-1)(x-y+z-1)}{4(1-z)}\\ {w}_{3}=\frac{(x+y+z-1)(x-y+z-1)}{4(1-z)}\\ {w}_{4}=\frac{(x+y+z-1)(-x+y+z-1)}{4(1-z)}\\ {w}_{5}=z\end{array}\)

13-knot formula

\(\begin{array}{}{w}_{1}=\frac{(-x+y+z-1)(-x-y+z-1)(x-0\text{.}5)}{2(1-z)}\\ {w}_{2}=\frac{(-x-y+z-1)(x-y+z-1)(y-0\text{.}5)}{2(1-z)}\\ {w}_{3}=\frac{(x-y+z-1)(x+y+z-1)(-x-0\text{.}5)}{2(1-z)}\\ {w}_{4}=\frac{(x+y+z-1)(-x+y+z-1)(-y-0\text{.}5)}{2(1-z)}\\ {w}_{5}=\mathrm{2z}(z-0\text{.}5)\\ {w}_{6}=-\frac{(-x+y+z-1)(-x-y+z-1)(x-y+z-1)}{2(1-z)}\\ {w}_{7}=-\frac{(-x-y+z-1)(x-y+z-1)(x+y+z-1)}{2(1-z)}\end{array}\)

\(\begin{array}{}{w}_{8}=-\frac{(x-y+z-1)(x+y+z-1)(-x+y+z-1)}{2(1-z)}\\ {w}_{9}=-\frac{(x+y+z-1)(-x+y+z-1)(-x-y+z-1)}{2(1-z)}\\ {w}_{\text{10}}=\frac{z(-x+y+z-1)(-x-y+z-1)}{1-z}\\ {w}_{\text{11}}=\frac{z(-x-y+z-1)(x-y+z-1)}{1-z}\\ {w}_{\text{12}}=\frac{z(x-y+z-1)(x+y+z-1)}{1-z}\\ {w}_{\text{13}}=\frac{z(x+y+z-1)(-x+y+z-1)}{1-z}\end{array}\)

Numerical integration formula with 5 points of order 2 (FPG5):

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(\mathrm{0,5}\)	\(0\)		\({h}_{1}\)	\({p}_{1}\)
2	\(0\)	\(\mathrm{0,5}\)		\({h}_{1}\)	\({p}_{1}\)
3	\(–\mathrm{0,5}\)	\(0\)		\({h}_{1}\)	\({p}_{1}\)
4	\(0\)	\(–\mathrm{0,5}\)		\({h}_{1}\)	\({p}_{1}\)
5	\(0\)	\(0\)		\({h}_{1}\)	\({p}_{1}\)

with:

\({h}_{1}=0.1531754163448146\)

\({h}_{2}=0.6372983346207416\)

\({p}_{1}=\frac{2}{15}\)

Numerical integration formula with 6 order 3 points (FPG6):

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(0\)	\(0\)		\({h}_{1}\)	\({p}_{1}\)
2	\(0\)	\(0\)		\({h}_{2}\)	\({p}_{2}\)
3	\(–a\)	\(0\)		\({h}_{3}\)	\({p}_{3}\)
4	\(0\)	\(–a\)		\({h}_{3}\)	\({p}_{3}\)
5	\(0\)	\(a\)		\({h}_{3}\)	\({p}_{3}\)
6	\(a\)	\(0\)		\({h}_{3}\)	\({p}_{3}\)

With:

\(a=0.5610836110587396\)

\({p}_{1}=0.1681372559485071\)

\({p}_{2}=0.07500000404404333\)

\({p}_{3}=0.1058823516685291\)

\({h}_{1}=0.1681372559485071\)

\({h}_{2}=0.00000000567585\)

\({h}_{3}=0.1058823516685291\)

10-point numerical integration formula (FPG10) of order 4, see [2]:

Point	\(x\)	\(y\)		\(z\)	Weight
1	\(0\)	\(0\)		\({h}_{1}\)	\({w}_{1}\)
2	\(0\)	\(0\)		\({h}_{2}\)	\({w}_{2}\)
3	\(-a\)	\(-a\)		\({h}_{3}\)	\({w}_{3}\)
4	\(-a\)	\(a\)		\({h}_{3}\)	\({w}_{3}\)
5	\(a\)	\(a\)		\({h}_{3}\)	\({w}_{3}\)
6	\(a\)	\(-a\)		\({h}_{3}\)	\({w}_{3}\)
7	\(-b\)	\(0\)		\({h}_{4}\)	\({w}_{4}\)
8	\(0\)	\(-b\)		\({h}_{4}\)	\({w}_{4}\)
9	\(0\)	\(b\)		\({h}_{4}\)	\({w}_{4}\)
10	\(b\)	\(0\)		\({h}_{4}\)	\({w}_{4}\)

With:

\(a=0.3252907781991163\)

\(b=0.65796699712169\)

\({h}_{1}=0.6772327888861374\)

\({h}_{2}=0.1251369531087465\)

\({h}_{3}=0.3223841495782137\)

\({h}_{4}=0.0392482838988154\)

\({w}_{1}=0.07582792211376127\)

\({w}_{2}=0.1379222683930349\)

\({w}_{3}=0.07088305859288367\)

\({w}_{4}=0.04234606044708394\)

Numerical integration formula with 15 Gauss points (FPG15) of order 5:

Point	\(x\)	\(y\)		\(z\)	Weight
1	0.0	0.0	0.0	0.7298578807825067	0.0456235799393942674
2	0.0	0.0	0.0	0.300401020813769	0.112931409661816
3	0.0	0.0	0.0	0.0000000064917722	0.03913635721904967
4	-0.3532630157731623	-0.3532630157731623	0.125	0.050960862086209874681
5	-0.3532630157731623	0.3532630157731623	0.125	0.050960862086209874681
6	0.3532630157731623	0.3532630157731623	0.125	0.05096086209874681
7	0.3532630157731623	-0.3532630157731623	0.125	0.050960862086209874681
8	-0.705117122727788277	0.531059878383280	0.061111907062023	0.0264472678827788277	0.02644726771976367
9	0.0	-0.705117121227788277	0.061111907062023	0.02644726771976367
10	0.0	0.705117121227788277	0.061111907062023	0.02644726771976367
11	0.705117122727788277	0.0	0.061111907062023	0.02644726771976367
12	-0.432882864103541	0.0	0.4236013371197248	0.011774414962347
13	0.0	-0.432882864103541	0.4236013371197248	0.011774414962347
14	0.0	0.432882864103541	0.4236013371197248	0.041951149272741
15	0.432882864103541	0.0	0.4236013371197248	0.041951149272741

Numerical integration formula with 24 Gauss points (FPG24) of order 6:

Point	\(x\)	\(y\)		\(z\)	Weight
1	0.0	0.0	0.0	0.8076457976939595	0.01697526244176133
2	0.0	0.0	0.0	0.0017638088528196	0.0107023421167942
3	0.0	0.0	0.0	0.1382628064637306	0.0797197029683492
4	0.0	0.0	0.0	0.4214239119356371	0.0687071134661012
5	-0.4172976755573542	-0.4172976755573542	0.097447341025462	0.024633755573542	0.02463375557353542	0.024633755573542
6	-0.4172976755573542	0.4172976755573542	0.097447341025462	0.024633755573542	0.02463375557353542	0.4172976755573542	0.097447341025462	0.024633755573542
7	0.4172976755573542	0.4172976755573542	0.097447341025462	0.024633755573542	0.02463375557353542	0.4172976755573542	0.097447341025462	0.024633755573542
8	0.4172976755573542	-0.4172976755573542	0.097447341025462	0.024633755573542	0.02463375557353542	0.024633725573542
9	-0.2169627046883496	-0.2169627046883496	0.5660745906233009	0.02105846883496	0.02105838883496	0.0210583863632544886
10	-0.2169627046883496	0.2169627046883496	0.5660745906233009	0.0210583846883496	0.02105838883496	0.0210583863632544886
11	0.2169627046883496	0.2169627046883496	0.5660745906233009	0.02105838883496	0.0210583868632544886
12	0.2169627046883496	-0.2169627046883496	0.5660745906233009	0.02105838883496	0.0210583868632544886
13	-0.565680854444256755	0.0	0.0294777308457207	0.0248000862596322
14	0.0	-0.565680858544256755	0.0294777308457207	0.0248000862596322
15	0.0	0.565680858544256755	0.0294777308457207	0.0248000862596322
16	0.565680854444256755	0.0	0.0294777308457207	0.0248000862596322
17	-0.498079091780705	0.0	0.2649158632121295	0.049254923117951295125	0.04925492311795127
18	0.0	-0.498079079091780705	0.2649158632121295	0.04925492311795127
19	0.0	0.498079099091780705	0.2649158632121295	0.04925492311795127
20	0.498079091780705	0.0	0.2649158632121295	0.04925492311795125	0.04925492311795127
21	-0.9508994872144825	0.0	0.0	0.048249070631936	0.0028934404244966
22	0.0	-0.950899484872144825	0.048249070631936	0.0028934404244966
23	0.0	0.950899484872144825	0.048249070631936	0.0028934404244966
24	0.9508994872144825	0.0	0.048249070631936	0.0028934404244966