2. Benchmark solution#

The solution should show the absorption of an acoustic wave by the absorbing surface. The movement of the piston is a uniform translation along the \(x\) axis. Given the symmetry of the problem around this axis, we will obtain an identical pressure field in all planes \(x=\mathrm{Cte}\). Moreover, the absorbent border is orthogonal to this axis. The absorption of plane pressure waves under normal incidence is therefore studied. The [bib1] theory says that with a fluid paraxial border of order 1, this absorption is perfect. This is what we need to check with this reference solution.

By observing the evolution of the pressure at a given point in the mesh, we will therefore try to find in the signal obtained the duration of excitation and the return to rest after the passage of the wave, characteristic of its absorption.

2.1. Benchmark results#

In this paragraph we give the results obtained with*Code_Aster* in this configuration. We check that they are satisfactory and we take them as a reference for the future.

For the 3D case, they concern the evolution of pressure at a point of the fluid located \(150m\) from the piston in the direction \(x\) and at the center of the section in the plane \(\mathrm{yz}\). For the 2D case, the point is located \(40m\) from the piston along \(x\) and in the middle of the section in the direction \(y\) (in 2D, we take a shorter and refined mesh).

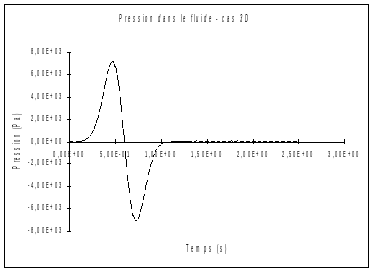
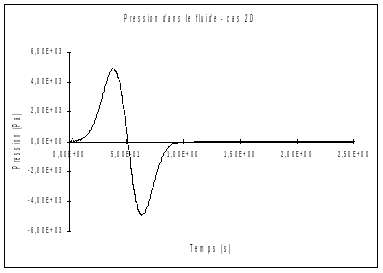
_images/100002000000017600000111A14690793407CA09.png _images/100002000000017F00000111D52AAFEE50F1E9E0.png

As expected, the width of the signal measured in both cases is identical to that of the excitation function. Physically, we can clearly observe the compression due to the advance of the piston, then the depression corresponding to its recoil to return to its initial position. We also clearly note the return to rest immediately after the wave has passed and the absence of a signal reflected at the end of the mesh.

2.2. Uncertainties#

It is a numerical study result. We find the qualitative forecasts. Numeric values are related to the accuracy of the calculation. Only the return to rest is clearly given by the analysis.

2.3. Bibliographical references#

    1. ENGQUIST, A. MAJDA « Absorbing boundary conditions for the numerical simulation of waves. » Mathematics of Computation (1977).