1. Reference problem

1.1. Geometry

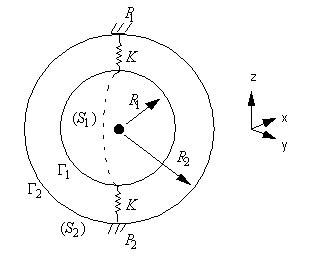
Inner sphere \(({S}_{1})\) has a radius \({R}_{1}=0.35m\).

Inner sphere \(({S}_{2})\) has a radius \({R}_{2}=0.45m\).

1.2. Material properties

Inner sphere \(({S}_{1})\) is made of steel:

\({\rho }_{s}=7800\mathrm{kg}/{m}^{3}\)

\(E=2.1{10}^{11}\mathrm{Pa}\)

\(\nu =0.3\)

The fluid filling the volume between \(({S}_{1})\) and \(({S}_{2})\) is water with a density of \({\rho }_{f}=\mathrm{1 000 }\mathrm{kg}/{m}^{3}\) (equivalent thermal characteristics: \(\lambda =1\), \({\rho }_{f}{C}_{p}=1000\)).

We go to model the fluid by 3D thermal modeling.

1.3. Boundary conditions and loads

A zero temperature is assumed at a point in the fluid mesh.

The springs are embedded at the level of the massif at points \({P}_{1}\) and \({P}_{2}\).