3. Modeling A#
3.1. Characteristics of modeling A#
The global coordinate system is chosen so that the discontinuity is horizontal in this coordinate system (\(\alpha =0°\) therefore an Euler angle of \(90°\)).
The modeling is carried out in plane deformation with 1092 elements QU4 for the mass and 91 elements QU4 for the discontinuity.
Discretization in time:
25 time steps for the first \(\mathrm{7,5}\) years
25 time steps for the next \(\mathrm{12,5}\) years.
3.2. Tested sizes and results#
The results obtained with*Code_Aster* are compared with those obtained by the code LAGAMINE.
We present the pressure profile along the discontinuity at \(\mathrm{7,5}\) and \(20\) years (figure), the variations in the opening along the discontinuity at \(\mathrm{7,5}\) and \(20\) years (figure) and the flow leaving the crack at the well per day (figure).
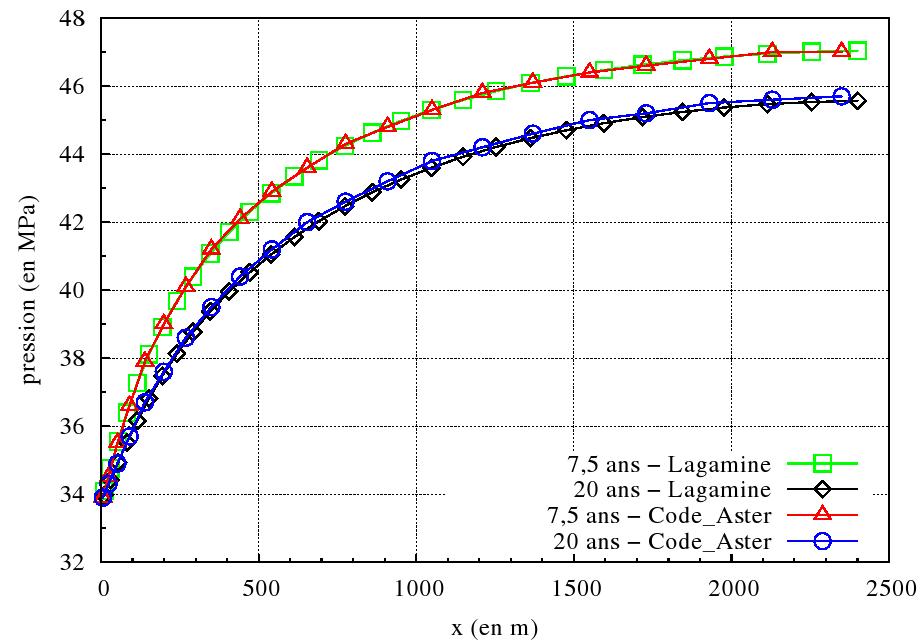
Figure 3.2.1: Pressure along the discontinuity at 7.5 years and 20 years and comparison with the results of LAGAMINE
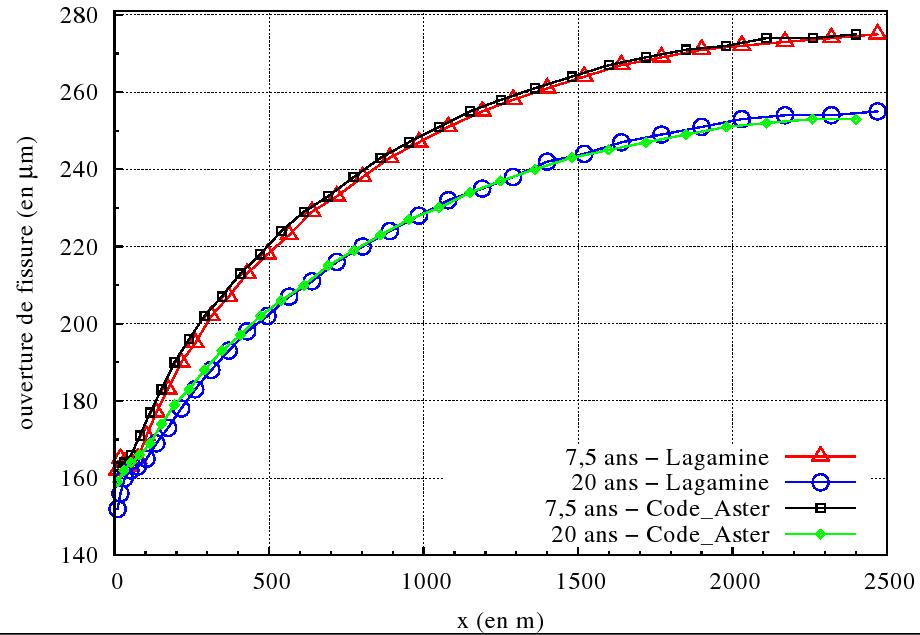
Figure 3.2.2: Opening of the discontinuity along the reservoir after 7.5 and 20 years and comparison with the results of LAGAMINE
The results are almost identical to those obtained with LAGAMINE.
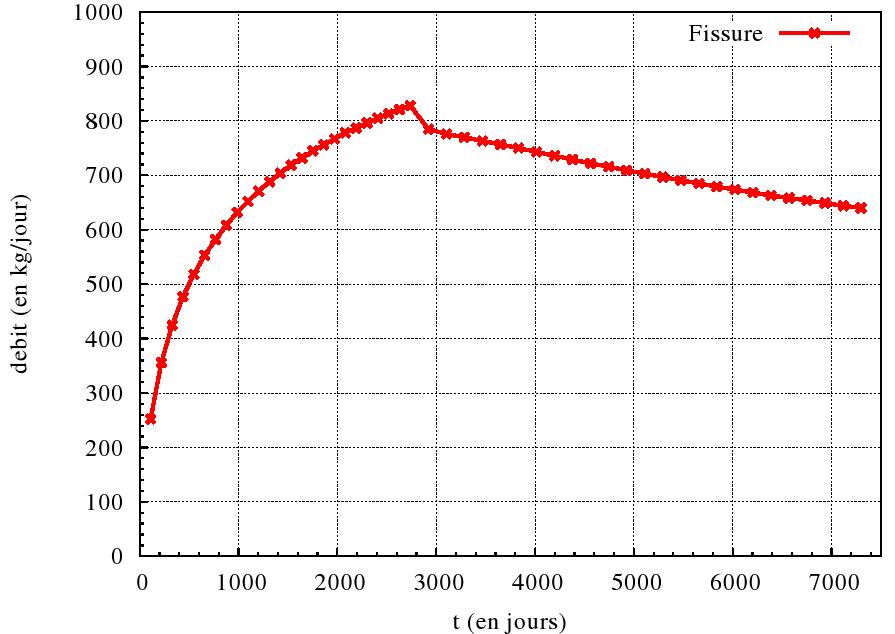
Figure 3.2.3: Mass flow out of the crack at the well per day over the time obtained with Code_Aster
The reference values are those obtained with LAGAMINE.
\(X(m)\) |
|
Time (years) |
Time (years) |
Reference \(\mathrm{PRE1}\) ( \(\mathrm{MPa}\) ) |
Tolerance ( \(\text{\%}\) ) |
256.97 |
0 |
7.5 |
7.5 |
39.95 |
|
516,51 |
0 |
7,5 |
42,68 |
|
|
256,97 |
0 |
20 |
20 |
38.45 |
|
516,51 |
0 |
20 |
40,98 |
|
\(X(m)\) |
|
Time (years) |
Reference \(\mathrm{V1}\) ( \(m\) ) |
Tolerance ( \(\text{\%}\) ) |
516,51 |
0 |
7,5 |
2,20E-04 |
|
516,51 |
0 |
20 |
2,04E-04 |
|
We add a case of non-regression:
\(X(m)\) |
|
Time (years) |
Reference \(\mathrm{FH11X}\) \(({\mathrm{kg.m}}^{-1}\mathrm{.}{s}^{-1})\) |
Tolerance ( \(\text{\%}\) ) |
516,51 |
0 |
7,5 |
-7,0189E-03 |
|
516,51 |
0 |
20 |
-5,3847E-03 |
|