7. E modeling#
7.1. Characteristics of modeling#
In this modeling, the aim is to start from a completely desaturated state (\(S\mathrm{=}\mathrm{0,0099}\) instead of \(S\mathrm{=}\mathrm{0,5}\) previously) in order to see the ability of the code to deal with this type of edge case. This makes it possible to validate the permeability regularization routines used in this case.
The law of hydraulic behavior is LIQU_AD_GAZ, everything else is identical to the modeling a (D_ PLAN_HH2MS).
The capillary pressure as a function of timecorresponding in the same way to the load of the problem:
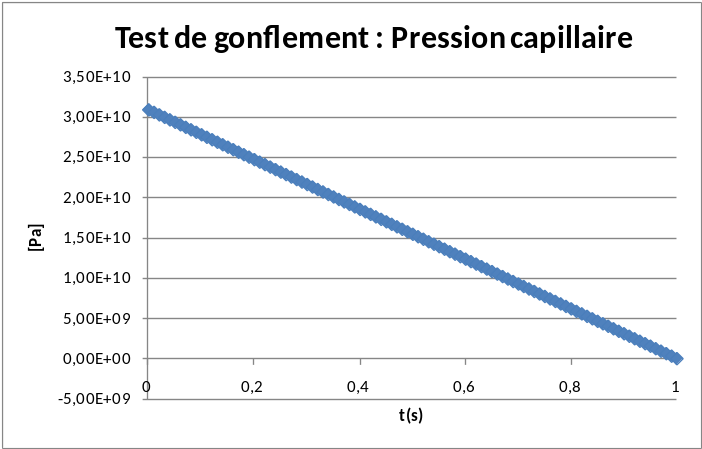
Figure 7.1- a : capillary pressure ( \(\mathit{N3}\) ****) **
7.2. Tested sizes and results#
The behavior is indeed that expected and corresponds to that observed in the previous simulations, except that the restoration is logically later.
This test case has no reference values, so we make it a non-regression case.
Tests are carried out on two values:
\(N\) |
Time ( \(s\) ) |
\(\mathit{SIXX}\) Aster |
\(N3\) |
|
|
\(N3\) |
|
|