1. Reference problem#
1.1. Geometry#
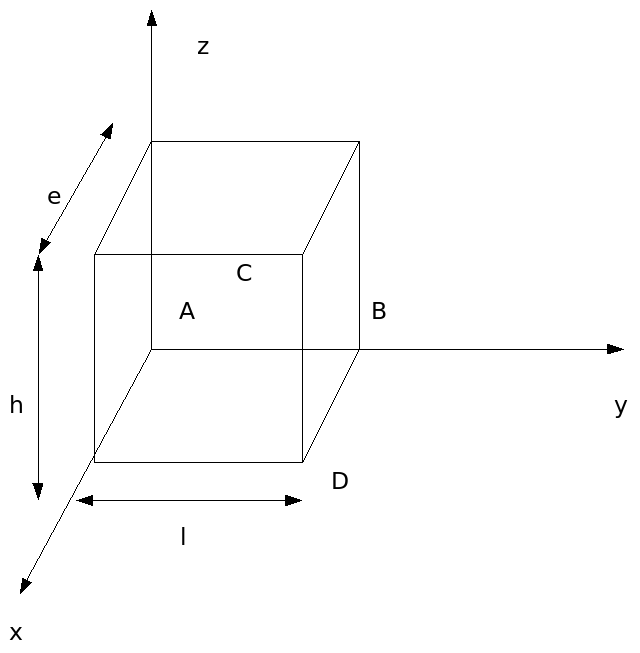
height: \(h=1m\)
width: \(l=1m\)
thickness: \(e=1m\)
Point coordinates (in meters):
\(A\) |
|
|
|
|
\(x\) |
0.5 |
|||
\(y\) |
0.5 |
|||
\(z\) |
0.5 |
1.2. Property of materials#
elastic properties under the keyword ELAS:
\(E\mathrm{=}5000.0\) in \(\mathrm{MPa}\)
\(\nu \mathrm{=}0.12\)
\(\alpha \mathrm{=}0.0\)
viscoplastic properties under the key VISC_DRUC_PRAG:
\({P}_{\mathit{ref}}\mathrm{=}0.1\) in \(\mathrm{MPa}\)
\(A\mathrm{=}1.5\mathrm{.}{10}^{\mathrm{-}12}\) in \({s}^{\mathrm{-}1}\)
\(n\mathrm{=}4.5\)
\({p}_{\mathit{pic}}\mathrm{=}0.015\)
\({p}_{\mathit{ult}}\mathrm{=}0.028\)
\({\alpha }_{0}\mathrm{=}0.065\)
\({\alpha }_{\mathit{pic}}\mathrm{=}0.26\)
\({\alpha }_{\mathit{ult}}\mathrm{=}0.091\)
\({R}_{0}\mathrm{=}1.3021\) in \(\mathrm{MPa}\)
\({R}_{\mathit{pic}}\mathrm{=}6.24808\) in \(\mathrm{MPa}\)
\({R}_{\mathit{ult}}\mathrm{=}1.30808\) in \(\mathrm{MPa}\)
\({\beta }_{0}\mathrm{=}\mathrm{-}0.15\)
\({\beta }_{\mathit{pic}}\mathrm{=}0.\)
\({\beta }_{\mathit{ult}}\mathrm{=}0.13\)
1.3. Initial conditions, boundary conditions, and loading#
Phase 1:
The sample is brought to a homogeneous state of effective stresses: \({\sigma }_{\mathrm{xx}}^{0}={\sigma }_{\mathrm{yy}}^{0}={\sigma }_{\mathrm{zz}}^{0}\), by imposing the corresponding total pressure on the front, right and upper faces and by imposing zero water pressures everywhere. The movements are blocked on the back (\({u}_{x}=0\)), left side (\({u}_{y}=0\)) and bottom (\({u}_{z}=0\)) faces.
Phase 2:
The movements are kept blocked on the rear (\({u}_{x}=0\)), left lateral (\({u}_{y}=0\)) and lower (\({u}_{z}=0\)) faces. On all sides, hydraulic flows are zero.
An imposed displacement is applied on the upper face in order to obtain a deformation \({\varepsilon }_{\mathit{zz}}\mathrm{=}\mathrm{-}\mathrm{0,06}\) (counted from the start of phase 2). On the front and right lateral faces, limit conditions under total stress are imposed:
\(\sigma \mathrm{.}n={\sigma }_{0}(=8\mathrm{MPa})\)