1. Reference problem#

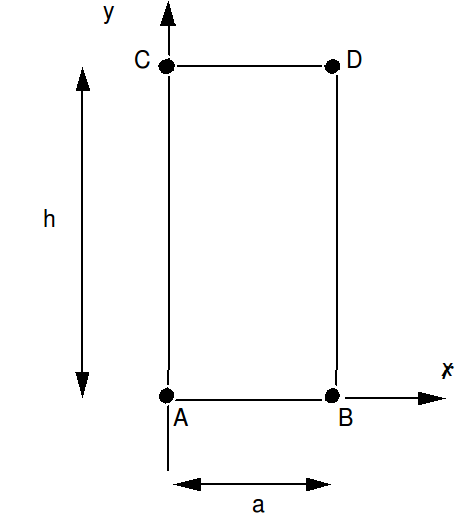
1.1. Geometry#

Width: \(a\mathrm{=}0.05m\)

Height: \(h\mathrm{=}0.2m\)

_images/10000000000001D600000206F8B564E4A5CA893F.png

1.2. Material properties#

The following convention is adopted in order to distinguish the parameters of the hot phase (austenitic) from the parameters of the cold phases (ferrito-pearlitic, bainitic and martensitic):

_images/Object_6.svg

=

Characteristics relating to the austenitic phase
_images/Object_7.svg

=

characteristics relating to the ferrito-pearlitic, bainitic and martensitic phases

Metallurgical parameters:

TRC to model a bainitic metallurgical evolution, over the entire structure, of the form:

\({Z}_{\mathit{fbm}}=\{\begin{array}{ccc}0.& \mathit{si}t\le {\tau }_{1}& {\tau }_{1}=60s\\ \frac{t-{\tau }_{1}}{{\tau }_{2}-{\tau }_{1}}& \mathit{si}{\tau }_{1}\le t<{\tau }_{2}& {\tau }_{2}=112s\\ 1.& \mathit{si}t\ge {\tau }_{2}& \end{array}\)

Thermal parameters:

Calorific capacity: \(\rho {C}_{p}=2.{10}^{6}{\mathit{J.m}}^{-3}\mathrm{.}°{C}^{-1}\)

Conductivity: \(\lambda =9999.9{\mathit{W.m}}^{-1}\mathrm{.}°{C}^{-1}\)

Thermo-mechanical parameters:

  • Thermo-elastic parameters:

Young’s module \(E=200000{10}^{6}\mathit{Pa}\)

Poisson’s ratio \(\nu =0.3\)

Thermal expansion coefficients

\({\alpha }_{\mathit{fbm}}=15.{10}^{-6}°{C}^{-1}\) \({\alpha }_{\mathit{aust}}=23.5{10}^{-6}°{C}^{-1}\)

Expansion coefficient definition temperature: \({T}_{\mathit{ref}}=900°C\)

Reference thermal deformation state: \(\Delta {\epsilon }_{f\gamma }^{{T}_{\mathit{ref}}}=2.52{10}^{-3}\)

Elastic limit:

\({\sigma }_{y}^{\mathit{fbm}}={\sigma }_{0}^{\mathit{fbm}}+{s}^{\mathit{fbm}}(T-{T}^{0})\) with \({\sigma }_{0}^{\mathit{fbm}}=530.{10}^{6}\mathit{Pa}\) and \({s}^{\mathit{fbm}}=0.5{10}^{6}\mathit{Pa.}°{C}^{-1}\)

\({\sigma }_{y}^{\mathit{aust}}={\sigma }_{0}^{\mathit{aust}}+{s}^{\mathit{aust}}(T-{T}^{0})\) with \({\sigma }_{0}^{\mathit{aust}}=400.{10}^{6}\mathit{Pa}\) and \({s}^{\mathit{aust}}=0.5{10}^{6}\mathit{Pa.}°{C}^{-1}\)

  • Thermoplastic parameters (law with linear work hardening)

Tangent modules: \({E}_{T}^{\mathit{fbm}}\) and \({E}_{T}^{\mathit{aust}}\) are chosen such that:

\({H}^{\mathit{fbm}}={H}_{0}^{\mathit{fbm}}+{\lambda }^{\mathit{fbm}}(T-{T}^{0})\) with \({H}_{0}^{\mathit{fbm}}=-50.{10}^{6}\mathit{Pa}\) and \({\lambda }^{\mathit{fbm}}=-5.{10}^{6}\mathit{Pa.}°{C}^{-1}\)

\({H}^{\mathit{aust}}={H}_{0}^{\mathit{aust}}+{\lambda }^{\mathit{aust}}(T-{T}^{0})\) with \({H}_{0}^{\mathit{aust}}=1250.{10}^{6}\mathit{Pa}\) and \({\lambda }^{\mathit{aust}}=-5.{10}^{6}\mathit{Pa.}°{C}^{-1}\)

We remind you that \(H=\frac{{\mathit{EE}}_{T}}{E-{E}_{T}}\)

  • Parameters for transformation plasticity:

Reminder:

In the case of a metallurgical evolution of the bainitic type, the model of transformation plasticity is as follows: \({\dot{\epsilon }}^{\mathit{pt}}=\frac{3}{2}\stackrel{̃}{\sigma }{k}^{\mathit{fbm}}{F}^{\text{'}}({Z}_{\mathit{fbm}}){\dot{Z}}_{\mathit{fbm}}\)

Model parameters: \({k}^{\mathit{fbm}}=1.{10}^{-10}{\mathit{Pa}}^{-1}\) and \({F}^{\text{'}}({Z}_{\mathit{fbm}})=2(1-{Z}_{\mathit{fbm}})\)

1.3. Boundary conditions and loads#

  • \({u}_{Y}\mathrm{=}0\) on the \(\mathit{AB}\) side; \({u}_{X}=0\) in \(A\).

  • \(T\mathrm{=}{T}^{0}+\mu t\), \(\mu \mathrm{=}\mathrm{-}5°{\mathit{C.s}}^{\mathrm{-}1}\) throughout the structure.

Ratings: \(\begin{array}{c}T({\tau }_{1})={T}_{1}\\ T({\tau }_{2})={T}_{2}\end{array}\)

  • The load on the structure is due to thermal and metallurgical expansion phenomena constrained in the \(z\) direction by the condition of plane deformations.

1.4. Initial conditions#

\({T}^{0}=900°C={T}^{\mathit{ref}}\)