1. Reference problem#
1.1. Geometry#
Axisymmetric cylinder (models \(A\) and \(E\)) or rectangular plate (modeling \(B\)) or straight pipe (models \(C\) and \(D\)), or beam (modeling \(F\)), or parallelepiped \(\mathrm{3D}\)
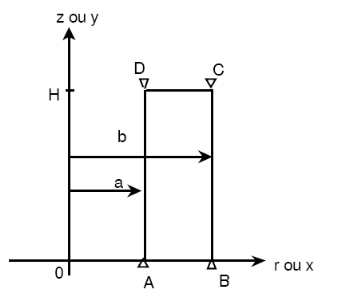
(models \(G\), \(H\) and \(J\)).
Cylinder geometry \((\mathrm{mm})\):
\(a=1\)
\(b=2\)
\(H=4\)
1.2. Property of the materials#
For all models:
Young’s module: \(E=200000\mathrm{MPa}\)
Tangent module: \({E}_{t}=50000\mathrm{MPa}\)
Poisson’s ratio: \(\nu =0.3\)
\({\sigma }_{0}=400\mathrm{MPa}\)
\(s=1.0{E}^{-2}°{C}^{-1}\)
Coefficient of thermal expansion: \(\alpha =1.0{E}^{-5}°{C}^{-1}\)
Volume heat: \({C}^{p}=0{\mathrm{J.mm}}^{-3}\mathrm{.}°{C}^{-1}\)
Thermal conductivity: \(\lambda =1.0{E}^{-3}{\mathrm{W.mm}}^{-1}\mathrm{.}°{C}^{-1}\)
For the isotropic material declared orthotropic, it comes:
E_L= E_T= E_N= \(E\)
nu_LT = nu_LN= nu_TN= \(\nu\)
G_LT= G_LN= G_TN= \(75000\mathrm{MPa}\)
ALPHA_L = ALPHA_T = ALPHA_N = \(\alpha\)
For models from \(A\) to \(G\):
\({\sigma }_{y}(T)={\sigma }_{0}(1-\mathrm{s.}(T-{T}_{0}))\)
For models \(H\) and \(I\):
\({\sigma }_{y}(T)\mathrm{=}{\sigma }_{0}\) \((s=0)\)
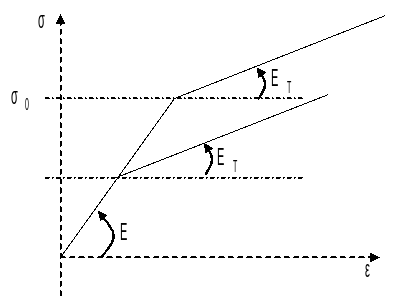
Figure: Material tensile curve
1.3. Boundary conditions and loads#
Models \(A\), \(E\) and \(K\): \(\mathrm{uz}=0\) on the sides \(\mathrm{AB}\) and \(\mathrm{CD}\) (Fixed \(\mathrm{Oz}\) axis)
Models \(B\) and \(I\): \(\mathrm{uy}=0\) on the sides \(\mathrm{AB}\) and \(\mathrm{CD}\), \(\mathrm{ux}=0\) in \(A\)
Models \(C,D\) and \(F\): embedding in \(A\), \(\mathrm{Uy}=0\) in \(C\)
Modelings \(G\), \(H\), \(L\), and \(M\): \(\mathrm{uy}=0\) on the sides \(\mathrm{AB}\) and \(\mathrm{CD}\), \(\mathrm{ux}=\mathrm{uz}=0\) (node \(\mathrm{N3}\)), \(\mathrm{uz}=0\) (node): on the sides and \(\mathrm{N4}\)
\(T(t)=\gamma t+\mathrm{T0}\) with: \(\gamma =1°C/s\) and \(\mathrm{T0}=0°C\).
Models \(H\) and \(I\): Initial deformation fields: \(\varepsilon =\alpha (T-{T}_{0})\mathrm{Id}\)
Modeling \(J\): Field of imposed deformations: \({\varepsilon }_{\mathrm{yy}}=0\)