1. Reference problem

1.1. Geometry

Hardware point

1.2. Material properties

Isotropic elasticity \(E\mathrm{=}184000\mathit{MPa}\) \(\nu =0.3\)

Isotropic work hardening
R_0	\(97.83\mathit{MPa}\)	B	51.3
Memory
10		Q_0	\(\mathrm{-}86.2\mathit{MPa}\)
ETA	0.14	Q_M	\(270.5\mathit{MPa}\)
Kinematic work hardening (modeling A)
C1	182392 MPa	G1_0	3079
C2	16678 MPa	G2_0	178.7

Viscosity of LEMAITRE
UN_SUR_K	\(1\mathrm{/}156.9{(\mathit{MPa}{S}^{1\mathrm{/}N})}^{\text{-1}}\)	N	6.84

Non-radiality effect
DELTA1	0.00306 2	DELTA2	0.01546

1.3. Boundary conditions and loads

Non-proportional traction-torsional loading, with imposed deformation, with increments of 15 degrees, which amounts to a material point in imposing components \({\varepsilon }_{\mathit{xx}}\) and \({\varepsilon }_{\mathit{xy}}\), with a phase difference between these two components. For each angle, the cycles are symmetric.

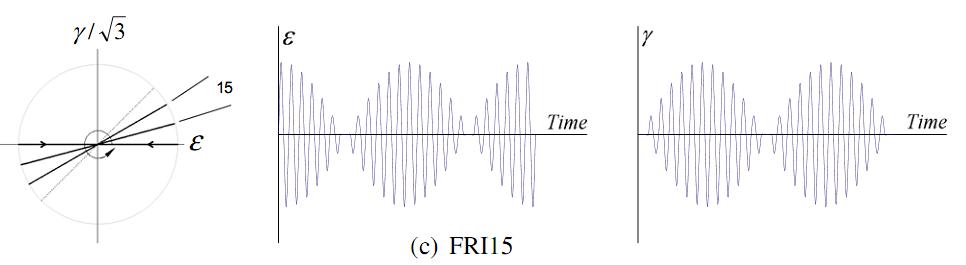
The representation of the load in a \(\frac{2}{\sqrt{3}}{\varepsilon }_{\mathit{xy}}\) - \({\varepsilon }_{\mathit{xx}}\) plane is as follows:

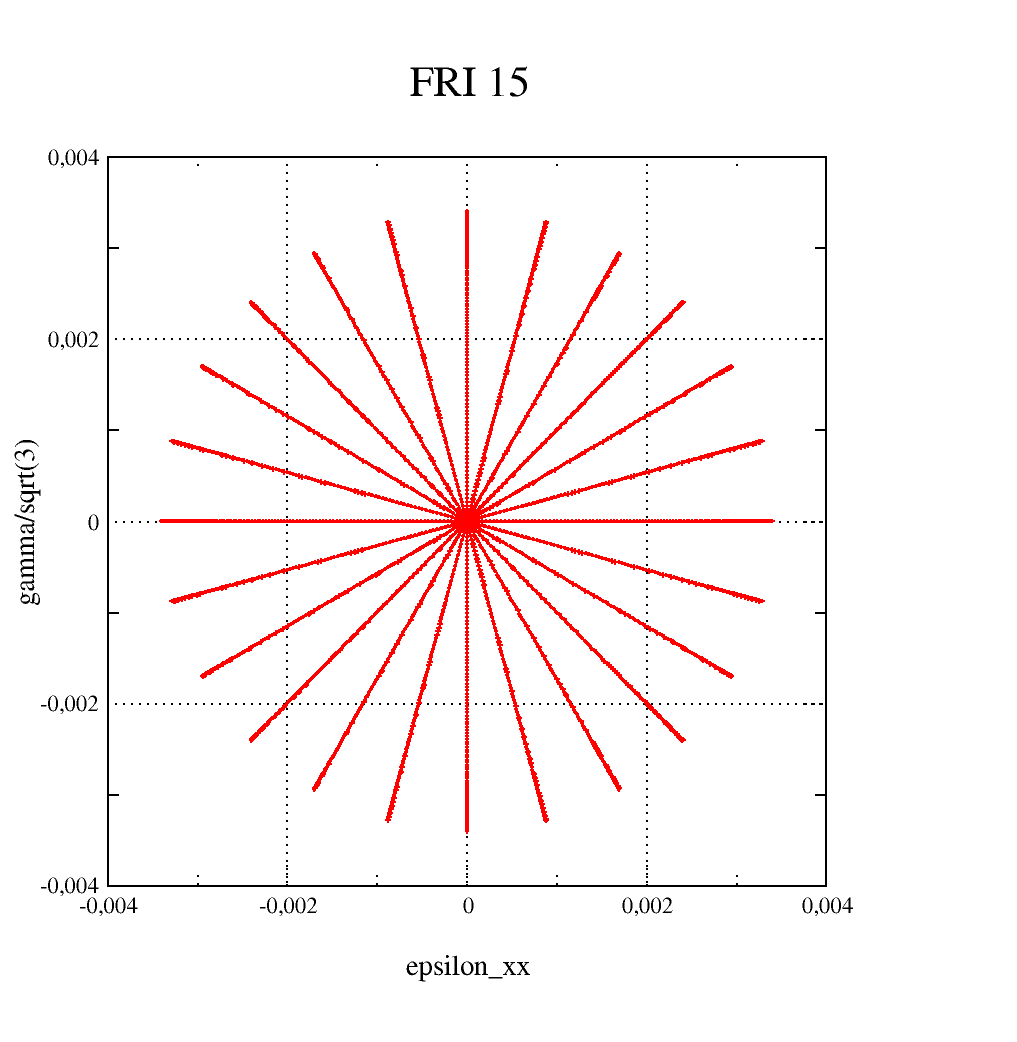
To obtain an almost stabilized state, all of these cycles are applied 4 times.