1. Reference problem#
1.1. Geometry#
It is a material point, representative of a state of homogeneous stresses and deformations.
It can be simulated by a volume element represented by a single finite element.
1.2. Material properties#
1.2.1. Isotropic elasticity coefficients#
\(E=173000\mathrm{MPa}\), \(\nu =0.3\) \(\mu =\frac{E}{2(1+\nu )}\)
1.2.2. Crystal law coefficients MONO_DD_CFC (A, B, C, E models)#
\(A\mathrm{=}0.13\)
\(B\mathrm{=}0.005\)
\(Y\mathrm{=}2.5E\mathrm{-}7\mathit{mm}(2.5\mathit{Angström})\)
\({\tau }_{f}\mathrm{=}20.\)
\(n\mathrm{=}50.\)
\(\dot{{\gamma }_{0}}\mathrm{=}{10}^{\text{-3}}\)
\({\rho }_{\mathit{ref}}\mathrm{=}{10}^{6}{\mathit{mm}}^{\text{-2}}\)
\(\alpha \mathrm{=}0.35\)
\(\beta \mathrm{=}{2.5410}^{\text{-7}}(2.54\mathit{Angström})\)
The interaction matrix is the one defined for MONO_DD_CFC [R5.03.11].
The family of sliding systems is octahedral (\(\mathit{CFC}\))
The coefficients related to irradiation (modeling E) are:
\(\begin{array}{}{\alpha }^{\mathrm{loops}}=0{\phi }^{\mathrm{loops}}=0.001{\alpha }^{\mathrm{voids}}=0{\rho }^{\mathrm{voids}}=1.e3\\ {\rho }_{\mathrm{sat}}=4{\rho }_{0}{b}^{2}{\phi }_{\mathrm{sat}}=0.04{\xi }_{\mathrm{irra}}={10}^{7}{\zeta }_{\mathrm{irra}}={10}^{7}\end{array}\) with \({\rho }_{0}={10}^{\text{6}}{\mathrm{mm}}^{\text{-2}}\)
The internal variables representing the dislocation density are initialized to \({\rho }_{0}\ast {b}^{2}\)
Those linked to irradiation have as initial values: \({\rho }_{s}^{\mathrm{loops}}=2{\rho }_{0}{b}^{2}\) \({\phi }_{s}^{\mathrm{voids}}=0.001\)
1.2.3. Crystal law coefficients MONO_DD_CC (D modeling)#
\({D}_{\mathit{LAT}}\mathrm{=}1.0\), \({K}_{\mathit{BOLTZ}}\mathrm{=}8.62E\mathrm{-}\mathrm{05,}\) \(\mathit{GAMMA0}\mathrm{=}1.E\mathrm{-}\mathrm{3,}{\mathit{TAU}}_{F}\mathrm{=}2.E7,\) \({\mathit{TAU}}_{0}\mathrm{=}3.63,\) \({\mathit{RHO}}_{\mathit{MOB}}\mathrm{=}1.E11,\) \({K}_{F}\mathrm{=}30.0,{K}_{\mathit{SELF}}\mathrm{=}100.0,\) \(B\mathrm{=}2.48E\mathrm{-}\mathrm{10,}\mathit{DELTAG0}\mathrm{=}0.84,D\mathrm{=}1.E\mathrm{-}\mathrm{08,}\) \(N\mathrm{=}20.0,\mathit{BETA}\mathrm{=}0.2,\) \(\mathit{GH}\mathrm{=}1.E11,{Y}_{\mathit{AT}}\mathrm{=}1.00E\mathrm{-}\mathrm{09,}\)
The interaction matrix is based on the following values
\(\mathit{H1}\mathrm{=}0.1024,\mathit{H2}\mathrm{=}0.7,\mathit{H3}\mathrm{=}0.1,\mathit{H4}\mathrm{=}0.1,\mathit{H5}\mathrm{=}0.1\mathit{H6}\mathrm{=}0.1,\)
The family of sliding systems is cubic1 (\(\text{CC}\)).
The internal variables representing the dislocation density are initialized to \({\rho }_{0}={10}^{\text{5}}{\mathrm{mm}}^{\text{-2}}\)
The formulation used here is formulation 1 (chosen using the parameter DELTA1 =0) (cf. [R5.03.11]
1.3. Boundary conditions and loads#
The cubic volume element on side \(\mathrm{1m}\) is subjected to a simple homogeneous tensile test, using imposed deformations.1 HEXA8.
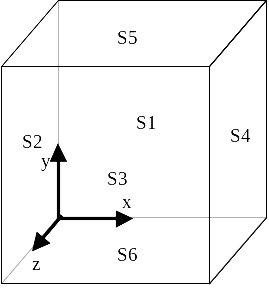
The imposed load is as follows:
Face \(\mathrm{S1}\) is blocked in the direction \(z\)
Face \(\mathrm{S3}\) is moved from \(\mathrm{0,2}\mathrm{mm}\) to \(0.2s\) and in 100 increments.
the movements following \(X\) and \(Y\) from the origin point are null
a stiffness equal to \({\mathrm{1O}}^{4}N/m\) according to \(Y\) is added to the origin point, via a discrete element, to allow an almost free rotation around \(Z\)
1.4. Initial conditions#
Zero stresses and deformations. Initial dislocation density: \({\rho }_{0}={10}^{6}{\mathrm{mm}}^{\text{-2}}\)