1. Reference problem#

1.1. Geometry#

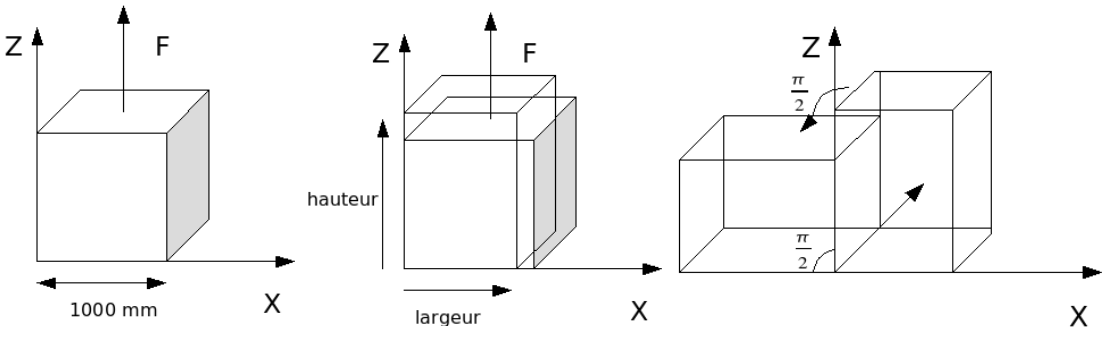
Figure1: Reference problem (for a \(90°\) rotation)

We consider a cubic element of matter with a side of \(1000\mathrm{mm}\) subjected alternately to a tensile force and then to an overall rotation of \(45°\). It undergoes a total of 4 traction/rotation cycles.

1.2. Material data#

Here we consider 6 elasto-plastic behavior laws with kinematic or combined kinematic/isotropic work-hardening of the von Mises type:

VMIS_CINE_LINE, VMIS_ECMI_LINE, VMIS_ECMI_TRAC,

VMIS_CIN1_CHAB and VMIS_CIN2_CHAB VMIS_CIN2_MEMO.

The table below lists the parameters used; in order to reinforce the comparison, the parameters used result in laws of behavior that are identical in all 5 cases (linear work hardening).

Keyword	Setting	Value
ELAS	E	\(200000\mathrm{MPa}\)
ELAS	NUDE	\(\mathrm{0,3}\)
TRACTION	SIGM	\((0.001\mathrm{,200});(0.002\mathrm{,202})\)
ECRO_LINE	D_ SIGM_EPSI	\(2000\mathrm{MPa}\)
ECRO_LINE	SY	\(200\mathrm{MPa}\)
PRAGER	C	\(\frac{2}{3}\frac{E\mathrm{\ast }\text{D\_SIGM\_EPSI}}{E\mathrm{-}\text{D\_SIGM\_EPSI}}\mathrm{\simeq }\mathrm{1346,8}\mathit{MPa}\)
CIN1_CHAB	C_I	\(\frac{E\mathrm{\ast }\text{D\_SIGM\_EPSI}}{E\mathrm{-}\text{D\_SIGM\_EPSI}}\mathrm{\simeq }\mathrm{2020,2}\mathit{MPa}\)
	R_0	\(200\mathit{MPa}\)
	R_I	\(200\mathit{MPa}\)
	G_0	\(0\)
CIN2_CHAB	C1_I	\(\frac{1}{2}\frac{E\ast \text{D\_SIGM\_EPSI}}{E-\text{D\_SIGM\_EPSI}}\simeq \mathrm{1010,1}\mathrm{MPa}\)
	C2_I	\(\frac{1}{2}\frac{E\ast \text{D\_SIGM\_EPSI}}{E-\text{D\_SIGM\_EPSI}}\simeq \mathrm{1010,1}\mathrm{MPa}\)
	R_0	\(200\mathrm{MPa}\)
	R_I	\(200\mathrm{MPa}\)
	G1_0	\(0\)
	G2_0	\(0\)

MEMO_ECRO	MU	0
	Q_M	0
	Q_0	0
	ETA	\(0\)

1.3. Boundary conditions and loads#

Two types of phases must be distinguished: traction phases and rotation phases. During the traction phases, the normal movements of the front and rear faces are blocked.

Traction phases:

First traction phase

Entity	Load Type	Value
Underside	FACE_IMPO	\(\mathrm{DNOR}=0\)
Top side	FACE_IMPO	\(\mathrm{DNOR}=\mathrm{500mm}\)
Rotation axis	DDL_IMPO	\(\mathrm{DX}=0\)
Front panel	FACE_IMPO	\(\mathrm{DNOR}=0\)
Back side	FACE_IMPO	\(\mathrm{DNOR}=0\)

Next pull-ups:

Entity	Load Type	Value
Underside	LIAISON_OBLIQUE	\(\mathrm{DZ}=0\)
Top side	LIAISON_OBLIQUE	\(\mathit{DZ}=300\mathit{mm}\)
Side \(X\mathrm{=}0\); \(Z\mathrm{=}\mathrm{1mm}\)	LIAISON_OBLIQUE	\(\mathrm{DX}=0\)
Rotation axis	DDL_IMPO	\(\mathrm{DX}=\mathrm{0,}\mathrm{DZ}=0\)
Front panel	DDL_IMPO	\(\mathrm{DY}=0\)
Back side	DDL_IMPO	\(\mathrm{DY}=0\)

Each traction phase is composed of 5 identical increments.

Rotation phase:

Boundary conditions

Entity	Load Type	Value
Rotation axis	DDL_IMPO	\(\mathrm{DX}=\mathrm{0,}\mathrm{DZ}=0\)
Front panel	DDL_IMPO	\(\mathrm{DY}=0\)
Back side	DDL_IMPO	\(\mathrm{DY}=0\)

The rotation load is imposed via a macro named CHAR_ROTA; an overall rotation of \(45°\) per phase is imposed, divided into 5 increments of \(9°\).

At the end of the loading, a deformation of 2,145 is obtained.