2. Benchmark solution

We assign to the discrete element, via the law of bilinear behavior, two stiffness \({K}_{1}\) and \({K}_{2}\) functions of the temperature of the form \({K}_{i}={\alpha }_{i}-{\beta }_{i}\dot{T}\).

Here we set arbitrarily:

\({\alpha }_{1}=2\dot{{\alpha }_{2}}={2.10}^{8}{\mathrm{N.m}}^{-1}\)

\({\beta }_{1}=2\dot{{\beta }_{2}}={4.10}^{6}{\mathrm{N.m}}^{-1}\)

We check that, regardless of the displacement \(U\) or the stress force \({F}_{P}\) that is imposed, we obtain a nodal reaction \(F\) of the discrete verifying the elastic law \(\Delta F={K}_{i}\mathrm{.}\Delta U\), where \(i=1\) if \(F\le {F}_{P}\) and \(i=2\) if \(F>{F}_{P}\).

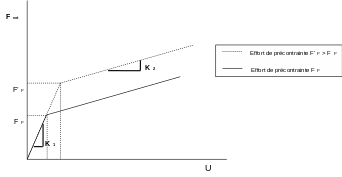
The discrete nodal reactions are recorded for displacements (\({U}_{1}<{U}_{2}\)) located on either side of the slope break.

Since the slope break takes place for \({U}_{P}={F}_{P}/{K}_{1}\), the reference solutions are obtained directly:

\({F}_{1}={K}_{1}\mathrm{.}{U}_{1}\) and \({F}_{2}={F}_{P}+{K}_{2}\mathrm{.}({U}_{2}-{U}_{P})\)

Be \({F}_{2}={F}_{P}\mathrm{.}(1-{K}_{2}/{K}_{1})+{K}_{2}\mathrm{.}{U}_{2}\)