4. B modeling

4.1. Characteristics of modeling

This modeling is strictly identical to the previous one, except for the elements used, which are quadratic.

4.2. Characteristics of the mesh

The square on which the modeling is performed is divided into 16 QUAD8. The interface is unmeshed and cuts the square horizontally.

4.3. Tested sizes and results

The results are obtained with*Code_Aster* (resolution with STAT_NON_LINE). We test the horizontal stress \({\sigma }_{\mathit{xx}}\), which is assumed to be uniformly zero, and the vertical stress \({\sigma }_{\mathit{yy}}\), which is assumed to be uniform, with a value of \(-E\). To do this, we test MIN and MAX of these two sizes throughout the element. The results obtained are summarised in the table below.

Tested quantities	Reference type	Reference values	Tolerance
SIGMAXX (MPa) MIN	“ANALYTIQUE”	0.0	0.01
SIGMAXX (MPa) MAX	“ANALYTIQUE”	0.0	0.02
SIGMAYY (MPa) MIN	“ANALYTIQUE”	-5800.0	0.002%
SIGMAYY (MPa) MAX	“ANALYTIQUE”	-5800.0	0.001%

The movements following \(y\) and the deformation are shown in Figure. A linear compression of the square is clearly observed, which takes place as if the crack were not present.

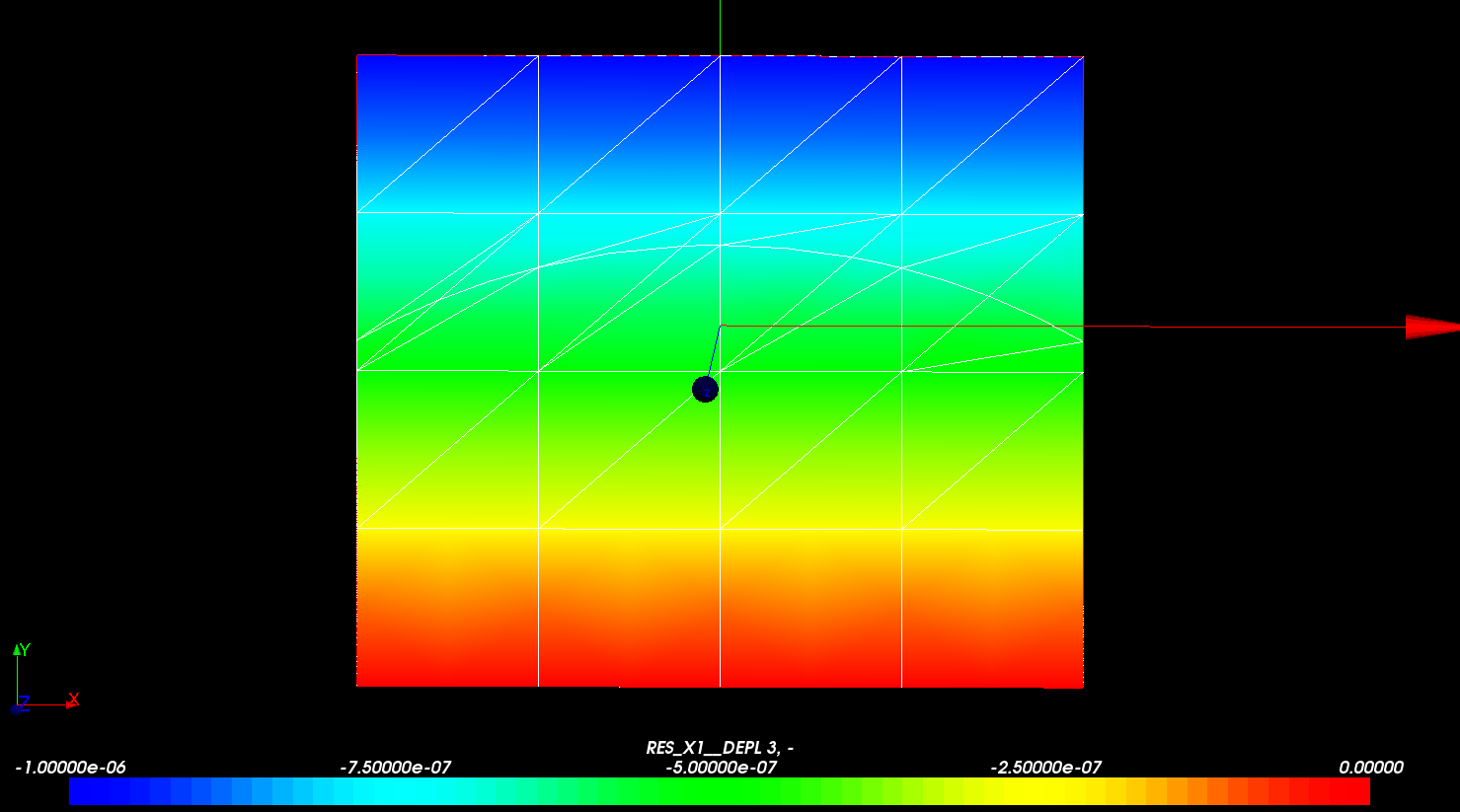
Figure 4.3-a : Field of movement by direction (Oy)

In Figures and, it is confirmed that the differences in constraints with respect to the analytical solution are significantly reduced compared to the previous linear modeling. The relative error decreases by a factor \(\mathrm{10⁵}\). Very slight differences are always observed in the vicinity of the crack and at the edges.

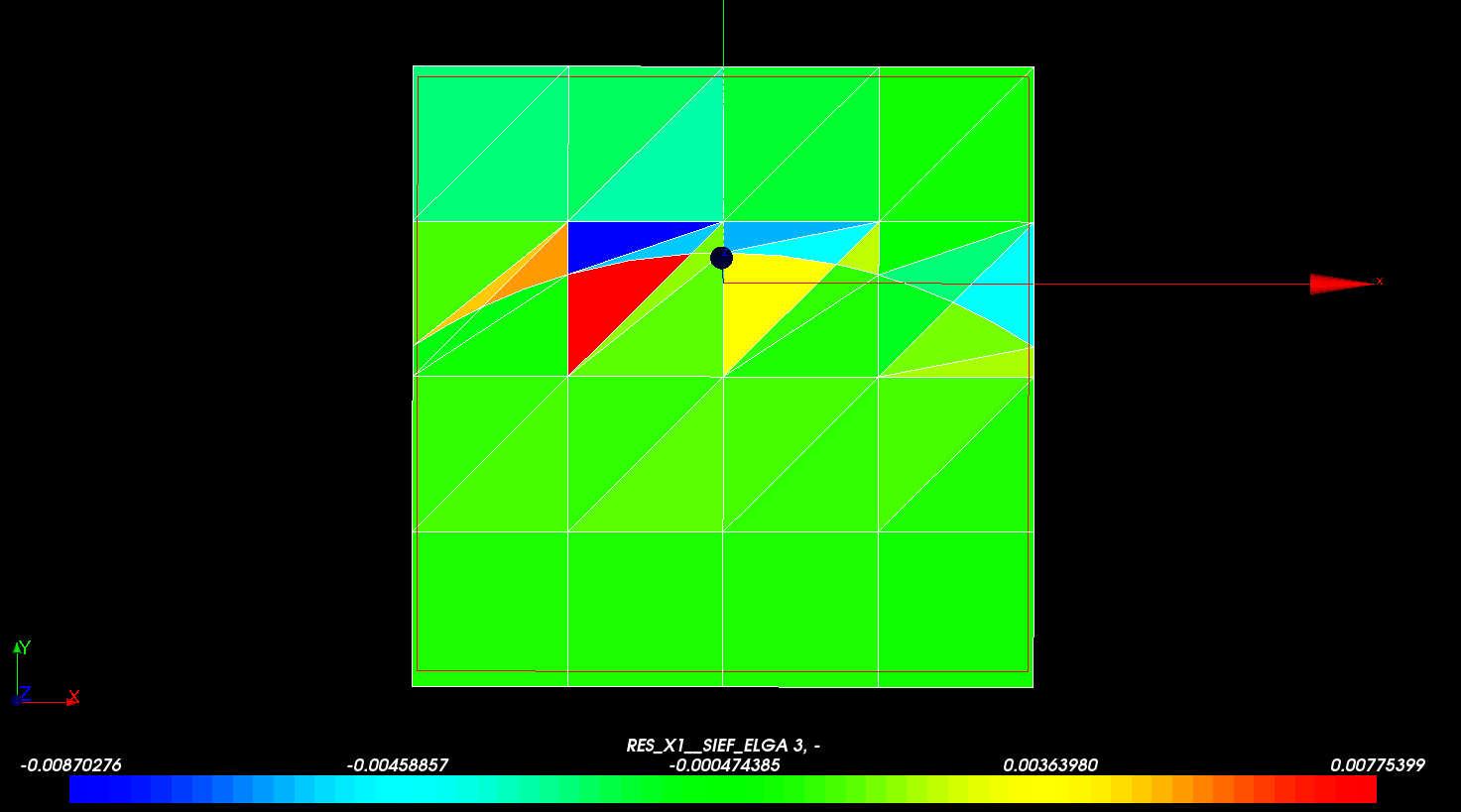
Figure 4.3-b : Constraint field sxx

Figure 4.3-c : Constraint field syy

The two previous models validate the use of contact facets from the integration sub-elements for the application of mechanical pressure and shear on the crack lips for 2D, linear and quadratic models. In particular, we note the significant gain in precision when using quadratic elements. Even if the discontinuity is curved, excellent precision is obtained with very few elements.