1. Reference problem#
1.1. Geometry#
The 2D structure is a unit square (\(\mathit{LX}\mathrm{=}1m\), \(\mathit{LY}\mathrm{=}1m\)), cut in two by a right interface located halfway up. [Figure 1.1-a on the left]. The 3D structure is a unit cube (\(\mathit{LX}\mathrm{=}1m\), \(\mathit{LY}\mathrm{=}1m\) and \(\mathit{LZ}\mathrm{=}1m\)), cut in two by a right interface located in the plane \(z\mathrm{=}\mathit{LZ}\mathrm{/}2\) [Figure 1.1-a on the right].
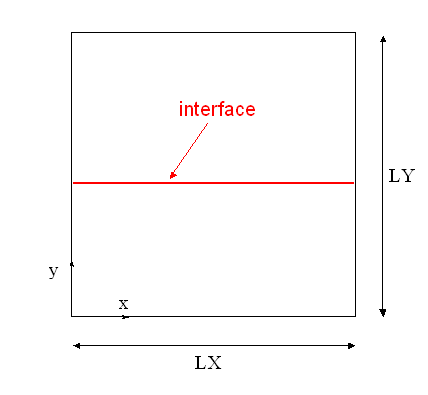
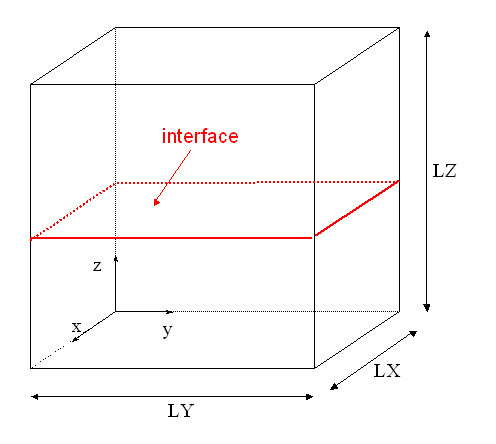
Figure 1.1-a : geometries of the square (left), of the cube (right)
1.2. Material properties#
Young’s module: \(E\mathrm{=}10000\mathit{MPa}\)
Poisson’s ratio: \(\nu \mathrm{=}0\)
1.3. Boundary conditions and loads#
A constant pressure load \(p\mathrm{=}10000\mathit{Pa}\) is applied to the interface (on both sides of the interface).
The movements of the nodes on the upper and lower faces are blocked in all directions.
1.4. Analytical solutions#
For constant pressure loading, everything happens as if there were two plates on either side of the interface in uniform compression. So the solution is analytical.
The move just above the level set is worth \({\nu }^{\text{+}}\mathrm{=}+\frac{p}{E}\frac{\mathit{LY}}{2}\) in 2D and \({\nu }^{\text{+}}\mathrm{=}+\frac{p}{E}\frac{\mathit{LZ}}{2}\) in 3D.
The move just below the level set is worth \({\nu }^{\text{-}}\mathrm{=}\mathrm{-}\frac{p}{E}\frac{\mathit{LY}}{2}\) in 2D and \({\nu }^{\text{+}}\mathrm{=}\mathrm{-}\frac{p}{E}\frac{\mathit{LZ}}{2}\) in 3D.