1. Reference problem#
1.1. Geometry#
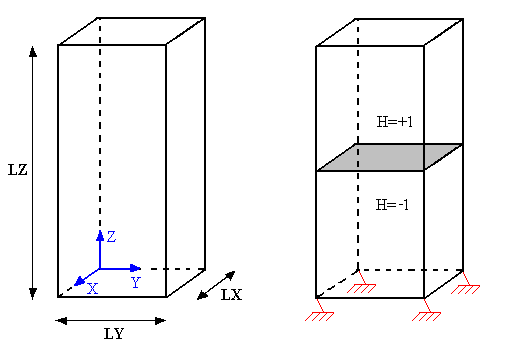
The structure is a straight parallelepiped with a rectangular and healthy base. The dimensions of the bar (see [Figure1.1-1]) are: \(\mathrm{LX}=2m\), \(\mathrm{LY}=4m\) and \(\mathrm{LZ}=10m\).
The interface (Figure 1.1-2) is introduced by level functions (normal level set noted \(\text{LN}\)) directly into the command file using the DEFI_FISS_XFEM [U4.82.08] operator. The interface is defined as a horizontal crack, in the middle of the block in the direction \(\mathrm{OZ}\) given by the following level function:
\(\text{LN}=Z-\mathrm{LZ}/2\) eq 1-1
1) 2)
Figure 1.1 Block geometry and crack positioning
No tangential level set is necessary since we use the keyword TYPE_DISCONTINUITE =” INTERFACE “, which makes it possible to have the structure completely divided into two parts.
1.2. Material properties#
Young’s module: \(E=100\mathrm{MPa}\)
Poisson’s ratio: \(\nu =0.0\)
Density: \(\rho =7800\mathrm{kg}/{m}^{3}\)
1.3. Boundary conditions and loading#
The nodes on the lower surface of the block are embedded (see Figures 1.1-1) by applying a loading in imposed displacements to the group of nodes of the surface:
\(\mathrm{ENCASTR}\): \(\mathrm{DX}=0\), \(\mathrm{DY}=0\), and \(\mathrm{DZ}=0\).
Two other loads, in imposed displacements, are applied to the group of nodes on the upper surface of the block:
\(\mathrm{CHZ}\): \(\mathrm{DZ}=\mathrm{DEPZ}\) and \(\mathrm{DX}=0\);
\(\mathrm{CHY}\): \(\mathrm{DY}=\mathrm{DEPY}\).
The values of the required trips are: \(\mathrm{DEPY}=\mathrm{DEPZ}=1.{10}^{-3}m\). Loads are applied in three steps using the functions shown on [].
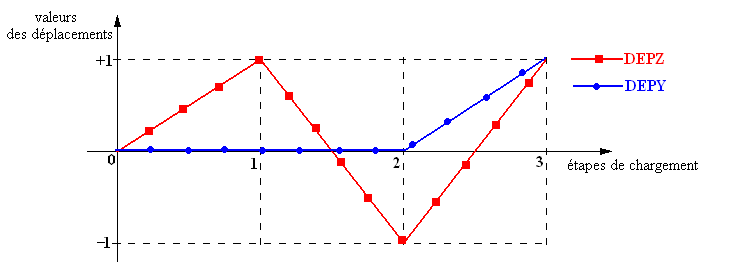
Figure 1.3-1: Variations in loads and imposed displacements
By imposing this movement kinematics at the top of the block, we want to show how option GLISSIERE works. In the initial state, the contact is not affected on the lips of the crack (CONTACT_INI =” NON “) and therefore the two parts of the block will separate following the first loading step (\(\mathrm{DZ}=\mathrm{DEPZ}\)). They stick together in the second stage when brought together (\(\mathrm{DZ}=-\mathrm{DEPZ}\)). Once in contact, option GLISSIERE is activated and prevents detachment in the normal direction (\(\mathrm{OZ}\)) during the third stage, despite the imposed displacement (\(\mathrm{DZ}=\mathrm{DEPZ}\)), tangential sliding at the interface level remains possible (\(\mathrm{DY}=\mathrm{DEPY}\)).