1. Reference problem#
1.1. Geometry#
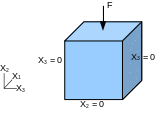
We consider a cube with side \(\mathrm{1m}\) which rests on a plane (\({x}_{2}=0\) on the lower face), subjected to pressure \(F\) on the upper face and in a situation of plane deformation following \({x}_{3}\) (\({x}_{3}=0\) on the right and left faces). The cube can therefore only be stretched along axis \({x}_{1}\)).
1.2. Material properties#
We test on three different materials, corresponding to three common models in hyper-elasticity.
Behavior ELAS_HYPER |
Mooney-Rivlin |
Neo-Hookean |
Signorin |
|
C10 |
0.709 |
1.2345 |
0.1234 |
|
C01 |
2.3456 |
0 |
1.2345 |
|
C20 |
0 |
0 |
0 |
0.456 |
NAKED |
0.499 |
0.499 |
0.499 |
1.3. Boundary conditions and loads#
|
: \(\mathrm{DY}=0\) |
|
: \(F=0.876\mathrm{Pa}\) |
|
: \(\mathrm{DZ}=0\) in 3D, nothing in D_ PLAN |
The load is increasing from \(F=0\) to \(F=\mathrm{0.876Pa}\), in 20 increments.