1. Reference problem#
1.1. Geometry#
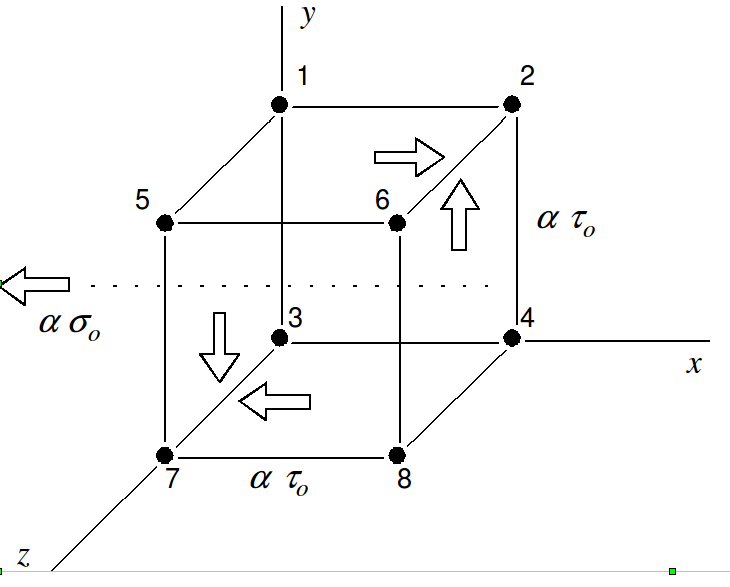
|
|
1.2. Material properties#
isotropic elasticity: |
\(E=206\mathrm{400.MPa}\) |
|
plasticity: (coefficients of the Rousselier model) |
\(D=2.\) \({f}_{0}\mathrm{=}{5.10}^{\mathrm{-}4}\) \({\sigma }_{1}=\mathrm{490.MPa}\) |
The rational traction curve is entered point by point with:
\(R(p)\mathrm{=}{r}_{i}+({r}_{0}\mathrm{-}{r}_{i}){e}^{\mathrm{-}\mathit{bp}}\)
with \(p\): cumulative plastic deformation
and \({r}_{i}\mathrm{=}1500\mathit{MPa}\)
\({r}_{0}\mathrm{=}\mathrm{520.MPa}\)
\(b=2.4\)
1.3. Boundary conditions and loads#
\(\mathrm{N04}\) |
|
Face \(\mathit{YZ}\): |
\(\mathrm{FX}=\mathrm{FY}=–F(t)\) |
\(\mathrm{N08}\) |
|
Face \(\mathrm{XZ}\): |
\(\mathrm{FX}=–F(t)\) |
\(\mathrm{N02},\mathrm{N06}\) |
|
Face \(\mathrm{1YZ}\): |
\(\mathrm{FY}=F(t)\) |
Face \(\mathrm{1XZ}\): |
\(\mathrm{FX}=F(t)\) |
409.707
1.4. Initial conditions#
Zero stresses and deformations at \(t=0\).