1. Reference problem#
1.1. Geometry#
It is a rectangular plate with a thickness of 1mm, with a hole and modelled with DKT DKT. Only a quarter of the plate is modelled thanks to symmetries. Dimensions are given in millimeters.
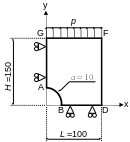
1.2. Boundary conditions and loads#
Symmetry conditions
The plate is stuck at \(\mathrm{Ox}\) along side \(\mathit{AG}\mathrm{:}\mathit{DY}=0.0,\mathit{DZ}=0.0,\mathit{DRY}=0.0\).
It is stuck at \(\mathrm{Oy}\) along side \(\mathit{BD}\mathrm{:}\mathit{DX}=0.0,\mathit{DZ}=0.0,\mathit{DRX}=0.0\).
Loading under imposed constraint
It is subject to traction \(p(t)\) following \(\mathrm{Oy}\) distributed on the side \(\mathrm{FG}\).
\(p(t=0)=0\), \(p(t=1000)=1000\).
We stop at the very beginning of plasticity at the edge of the hole, i.e. at 110s.
1.3. Material properties#
The behavior is Von Mises elastoplastic, with isotropic work hardening.
The elastic characteristics are:
Young’s module \(E=200000\mathrm{MPa}\);
Poisson’s ratio \(\nu =0.3\);
Elastic limit: \(200\mathrm{MPa}\);
Work hardening is deduced from the traction curve defined by the following data (constant straight extension PROL_DROITE =” CONSTANT “):
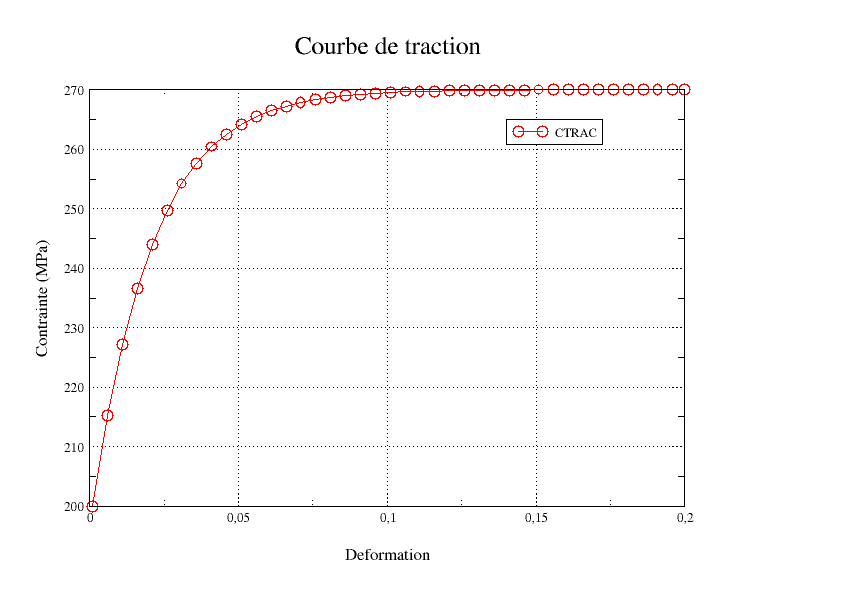
Epsilon |
Sigma ( \(\mathit{Mpa}\) ) |
Epsilon |
Sigma ( \(\mathit{Mpa}\) ) |
||
1.00000E-03 |
2.00000E+02 |
1.06000E-01 |
2.69626E+02 |
2.00000E+02 |
|
6.00000E-03 |
2.15275E+02 |
1.11000E-01 |
2.69709E+02 |
||
1.10000E-02 |
2.27253E+02 |
1.16000E-01 |
2.69773E+02 |
2.69773E+02 |
|
1.60000E-02 |
2.36630E+02 |
1.21000E-01 |
2.69823E+02 |
2.69823E+02 |
|
2.10000E-02 |
2.43964E+02 |
1.26000E-01 |
2.69862E+02 |
||
2.60000E-02 |
2.49694E+02 |
1.31000E-01 |
2.69893E+02 |
||
3.10000E-02 |
2.54168E+02 |
1.36000E-01 |
2.69917E+02 |
2.69917E+02 |
|
3.60000E-02 |
2.57659E+02 |
1.41000E-01 |
2.69935E+02 |
2.69935E+02 |
|
4.10000E-02 |
2.60382E+02 |
1.46000E-01 |
2.69949E+02 |
2.69949E+02 |
|
4.60000E-02 |
2.62506E+02 |
1.51000E-01 |
2.69961E+02 |
||
5.10000E-02 |
2.64161E+02 |
1.56000E-01 |
2.69969E+02 |
||
5.60000E-02 |
2.65451E+02 |
1.61000E-01 |
2.69976E+02 |
||
6.10000E-02 |
2.66457E+02 |
1.66000E-01 |
2.69981E+02 |
||
6.60000E-02 |
2.67240E+02 |
1.71000E-01 |
2.69986E+02 |
2.69986E+02 |
|
7.10000E-02 |
2.67850E+02 |
1.76000E-01 |
2.69989E+02 |
||
7.60000E-02 |
2.68325E+02 |
1.81000E-01 |
2.69991E+02 |
2.69991E+02 |
|
8.10000E-02 |
2.68696E+02 |
1.86000E-01 |
2.69993E+02 |
||
8.60000E-02 |
2.68984E+02 |
1.91000E-01 |
2.69994E+02 |
||
9.10000E-02 |
2.69209E+02 |
1.96000E-01 |
2.69996E+02 |
2.69209E+02 |
|
9.60000E-02 |
2.69384E+02 |
2.00000E-01 |
2.69996E+02 |
||
1.01000E-01 |
2.69520E+02 |
Table 1.3-1