1. Reference problem#

The problem comes from an article by J.C. Simo and.*M* .S. Raifai [1].

1.1. Geometry#

The geometry can be visualized in the figure and will be used for all models.

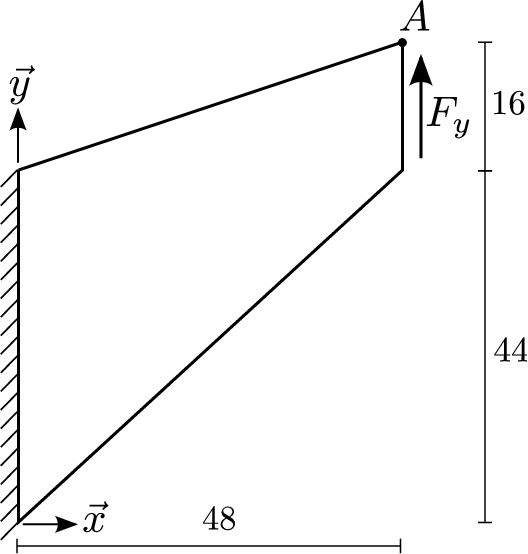
_images/10000201000002100000022AE3CEFA7E1D6B4F0C.png

Figure 1.1-1: Membrane geometry

Coordinate of Node A (48.60) and Node C (24.30).

1.2. Material properties#

The material is almost incompressible elastic, that is to say that its Poisson’s ratio tends to \(\mathrm{0,5}\):

  • Modulus of elasticity: \(E=70\mathit{MPa}\)

  • Poisson’s ratio: \(\mathrm{\nu }=\mathrm{0,499}\)

    The plasticity model is a Von Mises model with linear isotropic work hardening

  • Elastic limit: \(\mathit{SY}=\mathrm{0,243}\mathit{MPa}\)

  • Work hardening module: \(\mathit{ET}=\mathrm{0,13474}\mathit{MPa}\)

1.3. Boundary conditions and loads#

The left side of the membrane (\(\mathit{DX}=\mathit{DY}=0\)) is embedded, and a vertical surface force is applied on the right side such as \(\mathit{FY}=\mathrm{0,1125}\mathit{kN}/\mathit{mm}\mathrm{²}\)

1.4. Expansion to 3D#

The 3D extension is obtained by extruding in the \(z\) direction (\(1\mathit{mm}\) thickness). In addition, the movements along DZ are blocked in order to be reduced to the solution in plane deformations.