1. Reference problem#
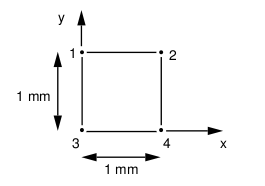
1.1. Geometry#
The homogeneous solution is obtained on a plane volume element (square with side \(1\)) or 3D (cube with side \(1\)) volume element. The dimensions have no influence on the solution.
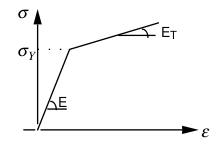
1.2. Material properties#
\(\begin{array}{c}E\mathrm{=}2.{10}^{7}\mathit{Pa}\\ \nu \mathrm{=}0.3\\ {\sigma }_{y}\mathrm{=}2.{10}^{8}\mathit{Pa}\\ {E}_{T}\mathrm{=}2.{10}^{9}\mathit{Pa}\end{array}\)
For diffusion, the material coefficients are, for a temperature of \(T\mathrm{=}293K\):
\(\begin{array}{c}{D}_{L}\mathrm{=}1.27{10}^{\text{-8}}\\ {N}_{L}\mathrm{=}5.1{10}^{29}{m}^{\text{-3}}\\ {K}_{T}\mathrm{=}{e}^{60000.\mathrm{/}\mathit{RT}}\\ {a}_{1}\mathrm{=}23.26{a}_{2}\mathrm{=}\mathrm{-}2.33{a}_{3}\mathrm{=}\mathrm{-}5.5\\ {V}_{h}\mathrm{=}2.e\mathrm{-}6R\mathrm{=}8.3144J\mathrm{/}\mathit{mol}\mathrm{/}K\end{array}\)
1.3. Boundary conditions and loads#
Side \(1\mathrm{-}3\) |
|
Side \(2\mathrm{-}4\): |
\({u}_{x}\mathrm{=}0.\) |
Point \(2\): |
\({u}_{y}\mathrm{=}0.\) |
Loading by a distributed force \({F}_{x}\) increasing over time:
Instant (\(s\)) |
0 |
|
|
Force \({F}_{x}\) |
0 |
|
|
Temporal discretization:
1 step until t= \({10}^{7}\)
100 steps until t= \({2.10}^{7}\): for each step, a mechanical calculation then a diffusion calculation.
The initial concentrations in \(\mathit{H2}\):
In the crystal lattice \({C}_{L}(0)\mathrm{=}2.08{10}^{21}{m}^{\text{-3}}\)
In the traps \({C}_{T}(0)\mathrm{=}8.42{10}^{20}{m}^{\text{-3}}\)