6. D modeling: 3D theoretical sawing#

6.1. Characteristics of modeling#

The simulation is carried out with 3D modeling_ JOINT. The elements are of type TETRA4 for the studs and PENTA6 for the joint elements. We test the two laws of behavior JOINT_MECA_FROT and JOINT_MECA_RUPT, the associated material has the same name. Surface elements are elastic.

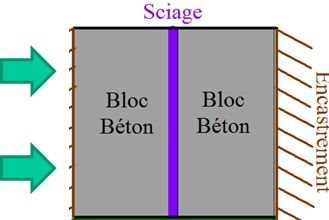
6.2. Characteristics of the mesh#

A linear unstructured mesh is produced by extruding mesh \(\mathrm{2D}\) (figure below).

Volume elements (pads): 2761 TETRA4

Attachments: 92 PENTA6

6.3. Tested sizes and results#

The first tests are carried out just before sawing in a condition where the joint and the studs are compressed homogeneously. Then the same series of tests are carried out after sawing. The values tested are profiles of joint thickness, as well as its opening and stress. We note \({\delta }_{n}\) (\(\mathit{V7}\)) the normal joint opening, joint thickness \({\delta }_{\mathit{offset}}\) (\(\mathit{V10}\)), as well as the normal stresses \({\sigma }_{n}\). The imposed degree of freedom is equal to \({\delta }_{\mathit{impo}}=-3e-6\), the saw thickness is equal to \({\delta }_{\mathit{scie}}={\delta }_{\mathit{impo}}/3\)

6.3.1. Before sawing, law JOINT_MECA_RUPT#

The solution is given by solving problem \(\mathrm{1D}\):

Size tested	“ ANALYTIQUE “	tolerance
\({\sigma }_{n}\) at height: \(5m\)	\({\delta }_{\mathit{impo}}/(\frac{1}{2LE}+\frac{1}{\text{pena\_contact}{K}_{N}})=-6.54545e5\)	0.1%
\({\delta }_{n}\) at height: \(2m\)	\(\frac{{\sigma }_{n}}{\text{pena\_contact}{K}_{N}}=-8.1818182e-7\)	0.1%

6.3.2. After sawing, law JOINT_MECA_RUPT#

The solution is given by solving problem \(\mathrm{1D}\):

Size tested	“ ANALYTIQUE “	tolerance
\({\sigma }_{n}\) at height: \(5m\)	\(({\delta }_{\mathit{impo}}+{\delta }_{\mathit{scie}})/(\frac{1}{2LE}+\frac{1}{\text{pena\_contact}{K}_{N}})=-4.363636e5\)	0.1%
\({\delta }_{\mathit{offset}}\) at height: \(8m\)	\(-{\delta }_{\mathit{scie}}=-1e-6\)	0.1%
\({\delta }_{n}\) at height: \(2m\)	\(\frac{{\sigma }_{n}}{\text{pena\_contact}{K}_{N}}-{\delta }_{\mathit{offset}}=-1.5454545e-6\)	0.1%

6.3.3. Before sawing, law JOINT_MECA_FROT#

The solution is given by solving problem \(\mathrm{1D}\):

Size tested	“ ANALYTIQUE “	tolerance
\({\sigma }_{n}\) at height: \(5m\)	\({\delta }_{\mathit{impo}}/(\frac{1}{2LE}+\frac{1}{{K}_{N}})=-6.923076923e-7\)	0.1%
\({\delta }_{n}\) at height: \(2m\)	\(\frac{{\sigma }_{n}}{{K}_{N}}=-6.923076923e-7\)	0.1%

6.3.4. After sawing, law JOINT_MECA_FROT#

The solution is given by solving problem \(\mathrm{1D}\):

Size tested	“ ANALYTIQUE “	tolerance
\({\sigma }_{n}\) at height: \(5m\)	\(({\delta }_{\mathit{impo}}+{\delta }_{\mathit{scie}})/(\frac{1}{2LE}+\frac{1}{{K}_{N}})=-4.6153846e5\)	0.1%
\({\delta }_{\mathit{offset}}\) at height: \(8m\)	\(-{\delta }_{\mathit{scie}}=-1e-6\)	0.1%
\({\delta }_{n}\) at height: \(2m\)	\(\frac{{\sigma }_{n}}{{K}_{N}}-{\delta }_{\mathit{offset}}=-1.46153846e-6\)	0.1%