1. Reference problem#
1.1. Geometry#
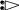


F1
D1
C1
B1
E1
A1

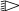
Ux
Linear relationships
1.2. Material properties#
The parameters of the laws of behavior are as follows:
For mechanical characteristics in linear elasticity (ELAS) :
Young’s module: |
\(E=31000\text{MPa}\) |
Poisson’s ratio: |
\(\nu \mathrm{=}0.2\) |
Coefficient of thermal expansion: |
\(\alpha \mathrm{=}{10}^{\mathrm{-}5}\) |
Desiccation shrinkage coefficient: |
\(\kappa \mathrm{=}{10}^{\mathrm{-}5}\) |
For the non-linear mechanical characteristics of the model **** BETON_DOUBLE_DP **** :
+——————————————————————-+——————————————————————————————————————+++ |*Uniaxial compression strength:* |:math:`f\text{'}c\mathrm{=}40N\mathrm{/}{\mathit{mm}}^{2}` ||| +——————————————————————-+——————————————————————————————————————+++ |*Uniaxial tensile strength:* |:math:`f\text{'}t\mathrm{=}4N\mathrm{/}{\mathit{mm}}^{2}` ||| +——————————————————————-+——————————————————————————————————————+++ |*Ratio of resistances in biaxial compression/uniaxial compression:*|\(\beta \mathrm{=}1.16\) ||| +——————————————————————-+——————————————————————————————————————+++ |*Breakdown energy in compression:* |:math:`\mathit{Gc}\mathrm{=}10\mathit{Nmm}\mathrm{/}{\mathit{mm}}^{2}` ||| +——————————————————————-+——————————————————————————————————————+++ |*Tensile breaking energy:* |:math:`\text{Gt}\mathrm{=}10000\mathit{Nmm}\mathrm{/}{\mathit{mm}}^{2}` ***to simulate almost zero work hardening* | +-------------------------------------------------------------------+------------------------------------------------------------------------------------------------------------------+++ |*Ratio of the yield strength to the uniaxial compression strength:*|\(33.33\text{\%}\) ||| +——————————————————————-+——————————————————————————————————————+++
For the mechanical characteristics of the linear work hardening model VMIS_ISOT_LINE :
+———————–+—————————————————————-+++ |*Elastic limit:* |:math:`\mathit{Sy}\mathrm{=}4N\mathrm{/}\mathit{mm²}` ||| +———————–+—————————————————————-+++ |*Work hardening slope:*|\(\text{D\_sigm\_epsi}\mathrm{=}0.1N\mathrm{/}\mathit{mm²}\) || +———————–+—————————————————————-+++
For the mechanical characteristics of the creep model of GRANGER ****: **
Coefficient \({J}_{1}\) : |
\({J}_{1}\mathrm{=}0.2{\mathit{MPa}}^{\mathrm{-}1}\) |
Coefficient \({\tau }_{1}\) : |
\({\tau }_{1}\mathrm{=}4320000s\) |
Coefficient \(Q\mathrm{/}R\) : |
\(\text{QsR\_K}\mathrm{=}0.\text{K}\) |
The desorption curve is equal to 1 for all values of humidity, to simplify the analytical solution. |
|
1.3. Boundary conditions and mechanical loads#
For calculations in \(\mathrm{3D}\):
|
stuck following \(\mathit{ox}\), |
|
stuck following \(\mathrm{oy}\), |
|
stuck following \(\mathrm{oz}\), |
|
|
|
|
|
Traction exerted following \(\mathit{ox}\). |
For calculations in \(\mathrm{2D}\):
|
stuck following \(\mathrm{ox}\), |
|
stuck following \(\mathrm{oy}\), |
|
|
|
|
|
Traction exerted following \(\mathrm{ox}\). |
The temperature field is either constant (first calculation) or increasing from \(0°C\) to \(20°C\) for all other calculations. In the case where the temperature varies, it is assumed that the drying field varies from 1 to 0. The material characteristics are constant. In addition, a non-zero desiccation shrinkage coefficient is applied, in such a way that the desiccation shrinkage compensates for thermal expansion, to verify that these 2 phenomena are properly taken into account.
**Note. The temperature variation impacts the calculation of withdrawals but not the law of mechanical behavior, which does not depend on temperature.*