4. B modeling#
4.1. Characteristics of modeling#
D_ PLAN (1 QUAD4, 2 , 2 , 2 TRI6) TRI3 UAD8
It is a 4-node square and two 3-node triangles linked by linear relationships to an 8-node square and two 6-node triangles. The assembly is subjected to uniaxial traction in direction \(x\). The dimensions following \(y\) are unitary. The dimensions in the \(x\) direction are chosen so that all elements have the same characteristic length (root of the area for quadratic elements, and root of the area multiplied by \(\sqrt{2}\) for linear elements).
The stress and deformation fields are uniform.
In \(\mathrm{2D}\) plane deformations (D_ PLAN), we test the coupling between the law BETON_DOUBLE_DPavec and the law GRANGER_FP. We are also testing the coupling of law VMIS_ISOT_LINE with law GRANGER_FP. The analytical solution was not calculated in D_ PLAN.
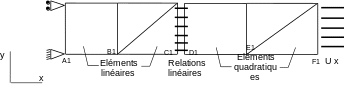
4.2. Characteristics of the mesh#
Number of knots: 20
Number of meshes and type: 1 QUAD4, 2 TRI3, 1 QUAD8, 2 TRI6
4.3. Tested features#
The components \(\mathit{xx}\) of the stress field SIGM_ELNO and of the creep deformation field EPFP_ELNO, and of the plastic deformation field EPSP_ELNO are tested at the point \(\mathit{F1}\) located at the end of the structure, where the imposed displacement is applied (en \({x}_{\mathit{max}}\)).
The analytical solution was not calculated using plane deformation. Therefore, only the same calculation is carried out with the 2 models of cracking with variable drying. The tests are of the non-regression type.
The tests are carried out at instant 10, when the plasticity has not started, only creep is present, and at time 100, after the start of the plasticization of the concrete.
4.3.1. Calculation with law BETON_DOUBLE_DP in non-isotherm (Non regression)#
These are non-regression tests, the values are not indicated.
In point \(\mathit{C1}\)
Variable tested |
\({\sigma }_{\mathit{xx}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}4}\) |
\({\varepsilon }_{\mathit{xx}}^{\mathit{fl}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}4}\) |
\({\sigma }_{\mathit{xx}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
\({\varepsilon }_{\mathit{xx}}^{\mathit{fl}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
\({\varepsilon }_{\mathit{xx}}^{p}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
In point \(\mathrm{F1}\)
Variable tested |
\({\sigma }_{\mathit{xx}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}4}\) |
\({\varepsilon }_{\mathit{xx}}^{\mathit{fl}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}4}\) |
\({\sigma }_{\mathit{xx}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
\({\varepsilon }_{\mathit{xx}}^{\mathit{fl}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
\({\varepsilon }_{\mathit{xx}}^{p}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
4.3.2. Calculation with law VMIS_ISOT_LINE in non-isotherm (Non regression)#
These are non-regression tests, the values are not indicated.
In point \(\mathrm{F1}\)
Variable tested |
\({\sigma }_{\mathit{xx}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}4}\) |
\({\varepsilon }_{\mathit{xx}}^{\mathit{fl}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}4}\) |
\({\sigma }_{\mathit{xx}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
\({\varepsilon }_{\mathit{xx}}^{\mathit{fl}}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |
\({\varepsilon }_{\mathit{xx}}^{p}\) for \({\varepsilon }_{\mathit{xx}}{10}^{\mathrm{-}3}\) |