2. Benchmark solution

2.1. Calculation method

The reference solution comes from the test case of the American software Plaxis2D [1] which calculates the stability factor using the SRM method (also available in CALC_STAB_PENTE, cf. [V6.03.507] and [U4.84.47]).

The Plaxis2D test case itself refers to the result provided by Verruijt via Bishop’s method simplified [2].

2.2. Benchmark result

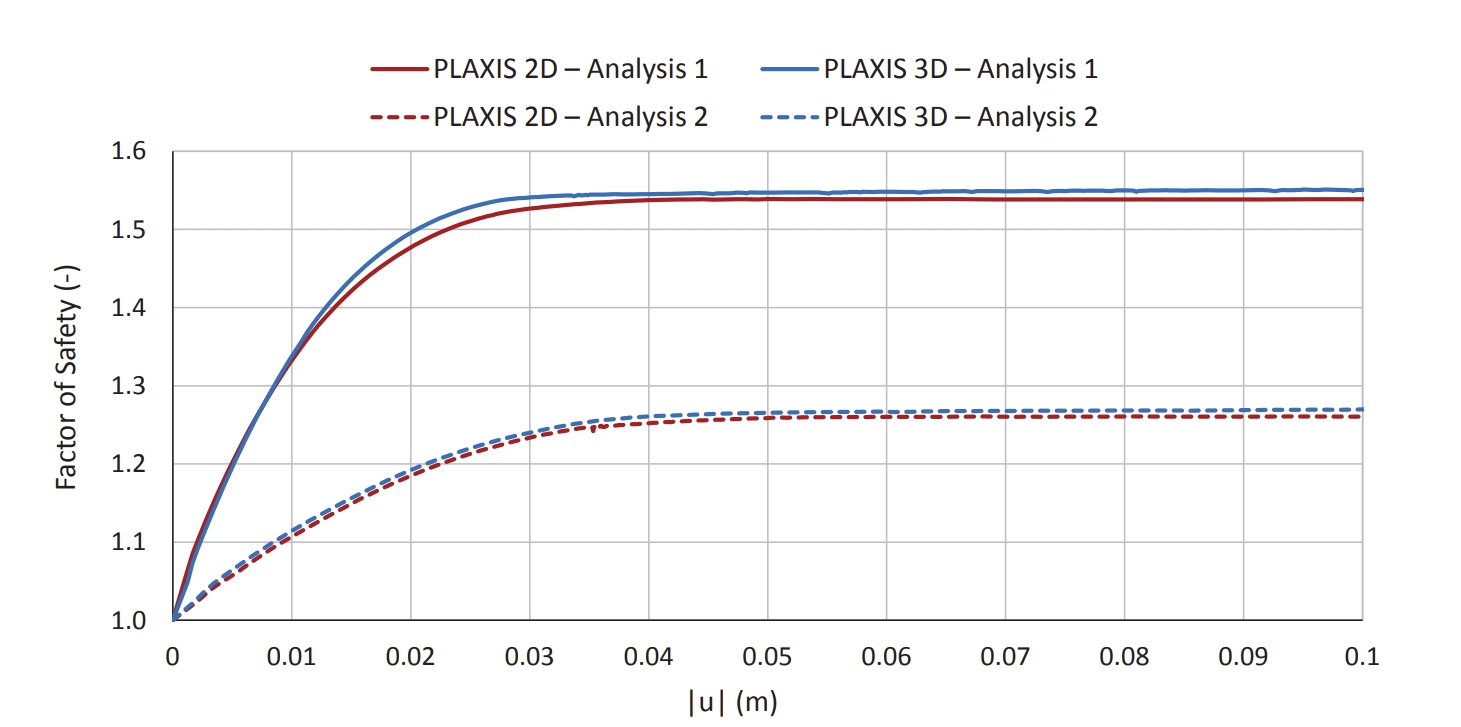
The result of Plaxis2D is shown in fig2-Plaxis. In method SRM, the FS is incremented up to the discrepancy of the nonlinear finite element calculation. Approaching the true FS value, the absolute displacement at the peak of the slope tends towards infinity, which implies the emergence of a plasticized zone forming the breaking surface that crosses the entire slope. The FS result is equal to 1.54 with the error tolerance 0.001.

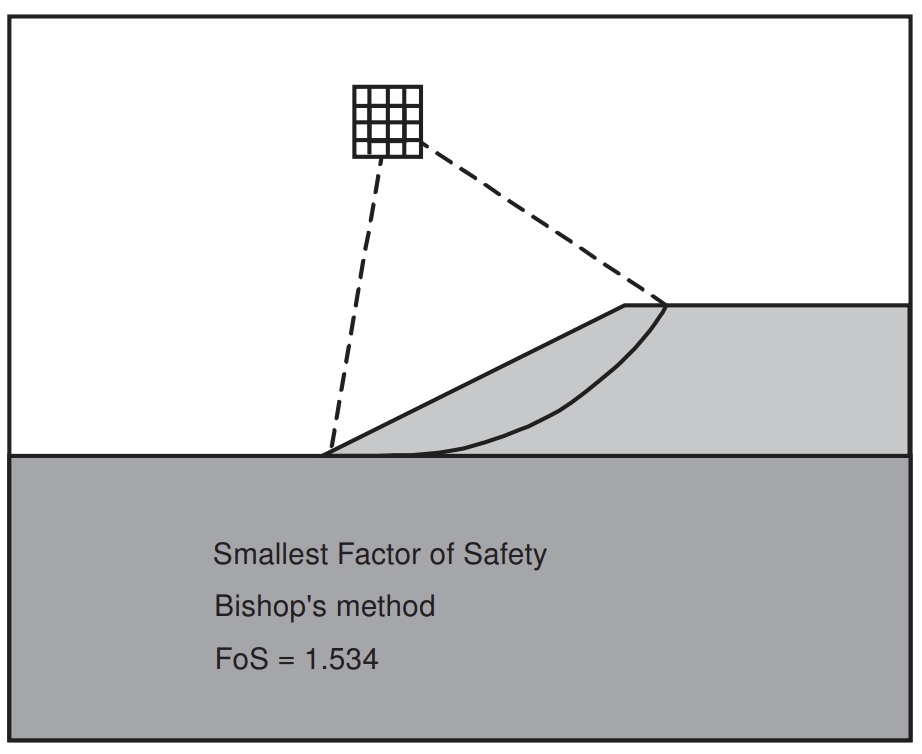
The fig3-Verruijt shows the result from the simplified Bishop method. We define in advance a grid of the possible centers of the sliding circles in order to find the one that minimizes FS. The FS obtained is equal to 1.534.