1. Reference problem

1.1 Geometry

As shown in Figure 1, the structure under investigation is a 2D plate containing a centrally placed crack. The crack is subjected to tensile loading conditions in the presence of initial stress fields.

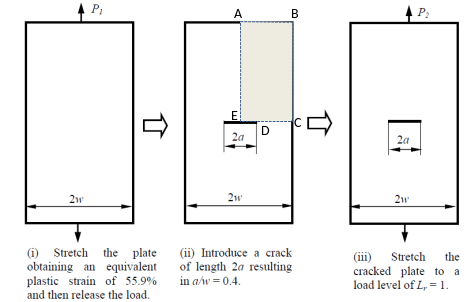
Figure 1: Geometry description.

The geometry parameters of this rectangular plate are a width, 2w = 50 mm, a height, 2h = 140 mm, and a crack length with the ratio a/w = 0.4.

Figure 1 also describes the shows the analysis sequence, which is split into three steps:

• Step 1: Uncracked plate is stretched beyond yielding until an equivalent plastic strain of 55.9% is achieved before the load is released. This generates an initial stress field.

• Step 2: A crack is introduced into the middle of the plate, and a dummy step run in order to produce an auto-equilibriated stress state in the plate.

• Step 3: The cracked plate is loaded again to 0.2% proof stress, thereby achieving a load lever Lr = 1.

1.2 Material Properties

For code_aster model to compute initial stress, the material is elastoplastic of Von Mises with a bi-linear strain-stress relationship

• Young modulus E = 500 MPa

• Plastic modulus Ep = (-y) /p

• Elastic limit y = 1 MPa

• E/Ep = 500

• Fish’s ratio = 0.3

1.3 Boundary conditions and loading

Thanks to symmetry, a quarter scale symmetric model of the geometry is considered, ABCDE (see Figure 1-ii). The boundary conditions applied to the different sides of the geometry during each step are shown below:

• • Step 1:

    • • AE: UX = 0

      • FROM: UY = 0

      • CD: UY=0

      • AB: P1 = -1.8 MPa

  • Step 2:

    • • AE: UX = 0

      • CD: UY=0

  • Step 3:

    • • AE: UX = 0

      • CD: UY=0

      • AB: P2 = -0.7 MPa

      • The stress obtained at the end of step 2 is introduced into step 3 as the initial stress.