1. Reference problem#
1.1. Geometry#
Lee’s gantry is a 2-armed gantry, articulated at its ends:
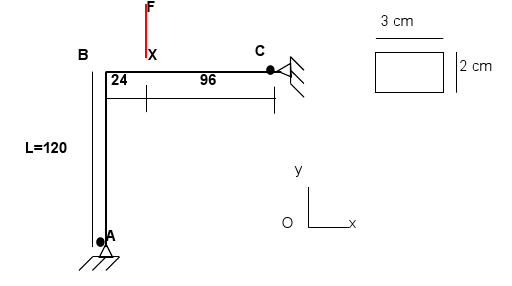
Coordinates of the points (in \(\mathrm{cm}\)):
\(A\) |
|
|
|
||
\(x\) |
0 |
0 |
0 |
120 |
24 |
\(y\) |
0 |
120 |
120 |
120 |
1.2. Characteristics of the section#
The arms have a rectangular cross section of \(3\mathrm{cm}\) by \(2\mathrm{cm}\). The section is oriented in such a way that the weakest inertia axis is perpendicular to the plane of the gantry.
\(A=6{\mathrm{cm}}^{2}\) |
\({I}_{y}=2.0{\mathrm{cm}}^{4}\) |
\({I}_{z}=4.5{\mathrm{cm}}^{4}\) |
\({A}_{y}=1.2\) |
\({A}_{z}=1.2\) |
1.3. Material properties#
\(E=720N/{\mathrm{cm}}^{2}\) |
\(\nu =0.3\) |
\({E}_{t}=72N/{\mathrm{cm}}^{2}\) |
\({\sigma }_{e}=10.44N/{\mathrm{cm}}^{2}\) |
1.4. Boundary conditions and loading#
Boundary conditions are imposed at points \(A\) and \(C\) (articulated around \(\mathrm{Oz}\)): \(\mathrm{DX}=\mathrm{DY}=\mathrm{DZ}=\mathrm{DRX}=\mathrm{DRY}=0\) |
|
We impose a vertical loading \(F\) on point \(X\): \(\mathrm{FY}=C\times t\) The constant \(C\) corresponds to the steering coefficient determined for example by an arc-length method. Indeed, this structure has a complex response under non-monotonic loading. |