1. Reference problem

1.1. Geometry

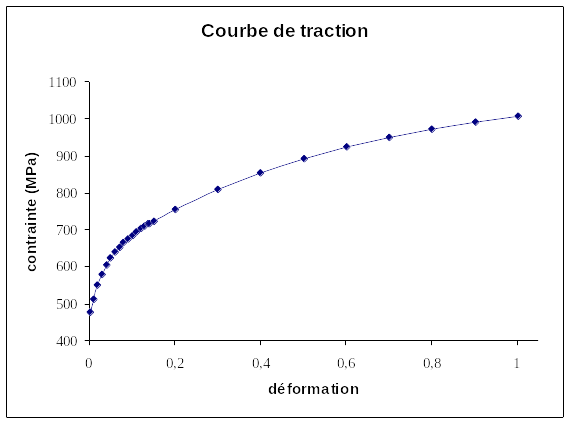
The aim is to test the 2 laws of viscoplastic behavior VISC_ISOT_TRAC and VISC_ISOT_LINE on a representative Elementary Volume \(R\) of dimension \(\mathrm{1mm}\), i.e. a cube in \(\mathrm{3D}\), the equivalent of a bar in plane deformations or of a cylinder in axisymmetry.

1.2. Material properties

Isotropic elasticity	Young’s modulus: Poisson’s ratio: \(\nu =0.3\)
Traction curve (mod. A, B and C)
Linear work hardening (mod. D, E, and F)
Coefficient for viscous law VISC_SINH
Rousselier model coefficients used to obtain the reference solution (mod. A, B and C)

1.3. Boundary conditions and loads

The volume element is subjected to a simple homogeneous tensile test. It is therefore stuck in \(x\) on the face [3,4] and in \(y\) on the face [1,3] (and possibly in the \(z\) direction) and subject to a displacement \(u(t)\) in the direction

on the face [1, 2].

3 values of \(T\) are used \(2000s\), \(0.2s\) and \(0.002s\), corresponding to deformation rates \(\dot{\varepsilon }\) of \({10}^{-3}{s}^{-1}\), \(10{s}^{-1}\) and \({10}^{3}{s}^{-1}\).

1.4. Initial conditions

Zero stresses and deformations at \(t=0\).