2. Benchmark solution#
2.1. Calculation method used for the reference solution#
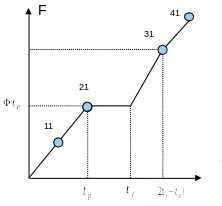
\(K\mathrm{=}{10}^{6}\), \(\frac{\Phi }{{\Phi }_{0}}\mathrm{=}1.698\)
\(F={\Phi }_{1}t\) \({\Phi }_{1}=7.2\times {10}^{21}\) if \(t\in [\mathrm{0,}{t}_{p}=1728.98]={I}_{1}\) \(\Rightarrow \Phi ={\Phi }_{1}\)
\(F={\Phi }_{1}{t}_{p}\) \({\Phi }_{1}=7.2\times {10}^{21}\) if \(t\in [:ref:`{t}_{p},{t}_{f}=2160.975 <{t}_{p},{t}_{f}=2160.975>\)] = {I} _ {2} :math:Rightarrow Phi =0`
\(F={\Phi }_{1}{t}_{p}+2{\Phi }_{1}(t-{t}_{f})\) \({\Phi }_{1}=7.2\times {10}^{21}\) if \(t\in [{t}_{f},{\mathrm{2t}}_{f}-{t}_{p}]={I}_{3}\) \(\Rightarrow \Phi =2{\Phi }_{1}\)
\(F={\Phi }_{1}t\) \({\Phi }_{1}=7.2\times {10}^{21}\) if \(t>({\mathrm{2t}}_{f}-{t}_{p})={I}_{4}\) \(\Rightarrow \Phi ={\Phi }_{1}\)
\(p={\left[\frac{n+m}{m}{\sigma }^{n}{(\frac{1}{K}\frac{\Phi }{{\Phi }_{0}}+L)}^{\beta }t{e}^{-\frac{Q}{R(T+{T}_{0})}}\right]}^{\frac{m}{n+m}}\) if \(t\in {I}_{1}\)
\(p={\left[\frac{n+m}{m}{\sigma }^{n}{(\frac{1}{K}\frac{\Phi }{{\Phi }_{0}}+L)}^{\beta }{t}_{p}{e}^{-\frac{Q}{R(T+{T}_{0})}}\right]}^{\frac{m}{n+m}}={p}_{f}\) if \(t\in {I}_{2}\)
\(p={p}_{f}\) to \(t={t}_{f}\) \(L=0\)
\(\dot{p}={\left[\frac{\sigma }{{p}^{\frac{1}{m}}}\right]}^{n}{(\frac{1}{K}\frac{2\Phi }{{\Phi }_{0}}+L)}^{\beta }{e}^{\frac{-Q}{R(T+{T}_{0})}}\)
\(\dot{p}{p}^{\frac{n}{m}}={\sigma }^{n}{(\frac{1}{K}\frac{2\Phi }{{\Phi }_{0}}+L)}^{\beta }{e}^{\frac{-Q}{R(T+{T}_{0})}}\)
\({\dot{p}}^{\frac{m+n}{m}}=\frac{m+n}{m}{\sigma }^{n}{(\frac{1}{K}\frac{2\Phi }{{\Phi }_{0}}+L)}^{\beta }{e}^{\frac{-Q}{R(T+{T}_{0})}}\)
\(p={\left[\frac{m+n}{m}{\sigma }^{n}{(\frac{1}{K}\frac{2\Phi }{{\Phi }_{0}}+L)}^{\beta }{e}^{\frac{-Q}{R(T+{T}_{0})}}((t-{t}_{f})2\beta +{t}_{p})\right]}^{\frac{m}{m+n}}\) if \(t\in {I}_{3}\)
\(p={\left[\frac{m+n}{m}{\sigma }^{n}{(\frac{1}{K}\frac{2\Phi }{{\Phi }_{0}}+L)}^{\beta }{e}^{\frac{-Q}{R(T+{T}_{0})}}(t+({t}_{f}-{t}_{p}(2\beta -2)))\right]}^{\frac{m}{m+n}}\) if \(t\in {I}_{4}\)
Digital app
\(\frac{1}{K}={10}^{-6}\); \(\frac{\Phi }{{\Phi }_{0}}=1.698\); \(\sigma =100\); \(\beta =1.2\)
To \(t=3456.96\)
\(p={(0.09067259953)}^{(\frac{m}{(n+m)})}=0.198332841\)
\(\varepsilon =0.200569905\)
To \(t=2592.97\)
\(p={(0.06882302104)}^{(\frac{m}{(n+m)})}=0.164696317\)
\(\varepsilon =0.166804179\)
2.2. Reference quantities#
Move \(\mathrm{DX}\) to node \(\mathrm{N02}\)
\(\mathrm{SIXX}\) constraint in \(\mathrm{MA1}\) mesh
Cumulative plastic deformation \(\mathrm{V1}\) in mesh \(\mathrm{MA1}\)
2.3. Benchmark result#
Size |
Knot or Knit |
Instant |
Reference |
\(\mathrm{V1}\) |
|
|
|
\(\mathrm{DX}(m)\) |
|
|
|
\(\mathrm{V1}\) |
|
|
|
\(\mathrm{DX}(m)\) |
|
|
|
\(\mathrm{SIYY}(\mathrm{Pa})\) |
|
|
|
2.4. Uncertainty about the solution#
Analytical solution