1. Reference problem#

1.1. Geometry#

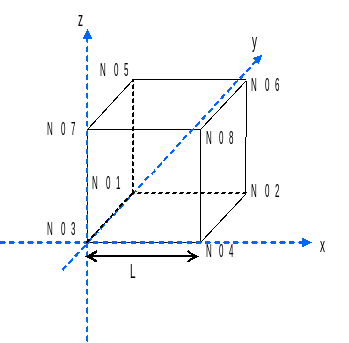
Cube geometry \((m)\): \(L=1\)

Coordinates of points \((m)\):

\(\mathrm{NO1}:(0.0,1.0,0.0)\) \(\mathrm{NO2}:(1.0,1.0,0.0)\) \(\mathrm{NO3}:(0.0,0.0,0.0)\) \(\mathrm{NO4}:(1.0,0.0,0.0)\) \(\mathrm{NO5}:(0.0,1.0,1.0)\) \(\mathrm{NO6}:(1.0,1.0,1.0)\) \(\mathrm{NO7}:(0.0,0.0,1.0)\) \(\mathrm{NO8}:(1.0,0.0,1.0)\)

mesh:

\(\mathrm{MA1}\): whole cube

1.2. Material properties#

- - Elastic
    \(E={10}^{5}\mathrm{Pa}\) Young’s module
    
    \(\nu =0.3\) Poisson’s ratio
    
    \(\alpha =0.\text{}/{}^{°}C\) Expansion coefficient
- - Lemaître
    \(\frac{1}{K}={10}^{-6}\)
    
    \(\frac{1}{m}=0.207060772\)
    
    \(n=2.3364\)
    
    \(L=0.\)
    
    \({\phi }_{0}=4.240281\times {10}^{21}\)
    
    \(\beta =1.2\)
    
    \(\mathrm{QSR}\text{\_}K=3321.093\)
    
    \(a=-1.51\times {10}^{-16}\)
    
    \(b=1.542\times {10}^{-13}\)
    
    \(S=0.396\)

1.3. Boundary conditions and loads#

- Imposed displacement \((m)\):
- - - \(\mathrm{N01}:\mathrm{DX}=\mathrm{DZ}=0\)
    - \(\mathrm{N03}:\mathrm{DX}=\mathrm{DY}=\mathrm{DZ}=0\)
    - \(\mathrm{N05}:\mathrm{DX}=0\)
    - \(\mathrm{N07}:\mathrm{DX}=0\)
- - Charging

The load is imposed on the \(\mathrm{N02},\mathrm{N04},\mathrm{N06},\mathrm{N08},\) nodes, varies progressively over the \(t\in [\mathrm{0,1}\mathrm{.}]\) interval and remains constant over the \(t\in \text{]}1.,32.{10}^{6}\text{]}\) interval as in the figure below.

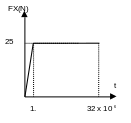
Fluence imposed on the nodes.

Instant \((s)\)	Fluence \(({\mathrm{n.m}}^{-2})\)
\(0.0\)
\(1.0\)	\(7.20000\times {10}^{21}\)
\(8.64990\times {10}^{2}\)	\(6.22793\times {10}^{24}\)
\(1.72898E+03\)	\(1.24487\times {10}^{25}\)
\(2.16097\times {10}^{3}\)	\(1.24487\times {10}^{25}\)
\(2.59297\times {10}^{3}\)	\(1.86694\times {10}^{25}\)
\(3.45696\times {10}^{3}\)	\(2.48901\times {10}^{25}\)

Temperature imposed on the knots.

\(T=299.85°C\) with a reference temperature of \({T}_{\mathrm{ref}}=299.85°C\)