1. Reference problem#
1.1. Geometry#
A discrete element of zero size with 2 knots.
Local coordinate system = global coordinate system.
A K_ TR_D_L stiffness matrix assigned by default (associated with an DIS_TR_L element)
\(1.6N/\mathrm{mm}\) in translation, \(1.9N/\mathrm{mm}\) in rotation.
The stiffness characteristics in the local directions \(x\) and rotation around \(y\) are modified by a behavior relationship of type ASSE_CORN introduced by a characteristic material.
1.2. Material properties#
Linked to an incremental behavior ASSE_CORN including 2 mechanisms each requiring 5 characteristic parameters (see [fig 1.2-a] and [fig 1.2-b]):
\(\stackrel{ˉ}{{N}_{1}}=10050N\), \(\stackrel{ˉ}{{M}_{1}}=150000\mathrm{N.mm}\), \(\stackrel{ˉ}{{U}_{1}}=1\mathrm{mm}\), \(\stackrel{ˉ}{{\theta }_{1}}=6.7{10}^{-2}\), \(\stackrel{ˉ}{{C}_{1}}=0.95\)
\(\stackrel{ˉ}{{N}_{2}}=50000N\), \(\stackrel{ˉ}{{M}_{2}}=750000\mathrm{N.mm}\), \(\stackrel{ˉ}{{U}_{2}}=10\mathrm{mm}\), \(\stackrel{ˉ}{{\theta }_{2}}=0.01\), \(\stackrel{ˉ}{{C}_{2}}=0.95\)
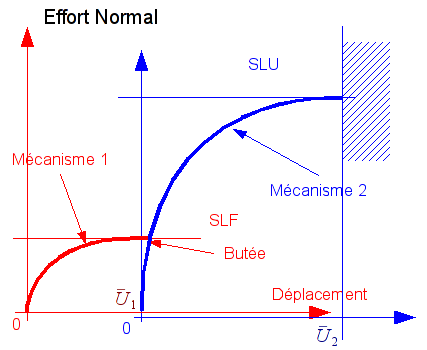
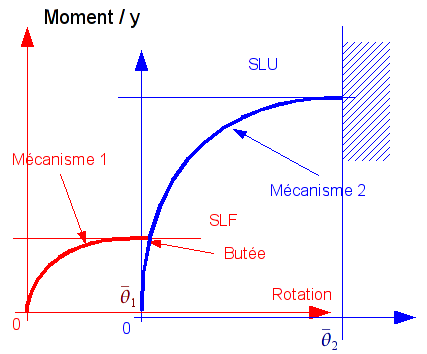
Figure 1.2-a : Assembly mechanisms under normal force and moment.
\(\begin{array}{}R(p)=\sqrt{\mathrm{n²}+\mathrm{m²}}\\ \dot{p}\cdot (\begin{array}{}n\\ m\end{array})=R(p)\cdot (\begin{array}{}\dot{{U}_{r}}\\ \dot{{\theta }_{r}}\end{array})\end{array}\)

|
\(n=\mathrm{Nx}/\stackrel{ˉ}{N}\)
|
Figure 1.2-b : Assembly behavior relationship
with
\(\begin{array}{ccc}\dot{p}& =& \sqrt{\dot{{U}_{r}^{2}}+\dot{{\theta }_{r}^{2}}}\\ p& =& {R}^{-1}(p\text{'})=h(p\text{'})=\frac{1-c}{{c}^{2}}\mathrm{.}\frac{{p}^{2}\text{'}}{1-p\text{'}}\end{array}\)
1.3. Boundary conditions and loads#
Embedding in one of the 2 knots.
Force imposed in the \(x\) direction per unit of \(\mathrm{1 000 }N\) and Moment imposed around the \(z\) axis per unit of \(\mathrm{3 000 }N\). All on the second node, in load increments.
1.4. Initial conditions#
Zero displacements, efforts, and internal variables.