1. Reference problem#
1.1. Geometry#
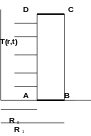
\({R}_{0}\) |
|
\({R}_{1}\) |
|
1.2. Material properties#
Young’s module: \(E=1\mathrm{MPa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Expansion coefficient: \(\alpha \mathrm{=}0.7\)
Law of LEMAITRE:
\(g(\sigma ,\lambda ,T)\mathrm{=}{(\frac{1}{K}\frac{\sigma }{{\lambda }^{\frac{1}{m}}})}^{n}\) with \(\frac{1}{K}\mathrm{=}1\), \(\frac{1}{m}\mathrm{=}0\), \(n\mathrm{=}1\)
1.3. Boundary conditions and loading#
Boundary conditions:
The cylinder is locked at \(\mathit{DY}\) on the \(\mathrm{[}\mathit{AB}\mathrm{]}\) and \(\mathrm{[}\mathit{CD}\mathrm{]}\) sides.
Charging:
The cylinder is subjected to a temperature field \(T(r,t)\mathrm{=}t{r}^{2}\)