1. Reference problem#
1.1. Geometry#
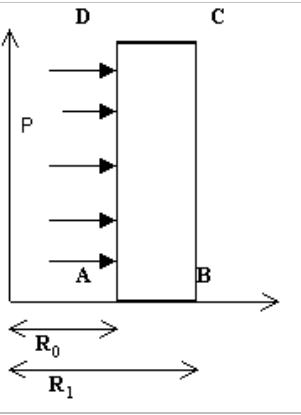
Cylinder dimensions: |
|
\({R}_{0}\) |
\(1m\) |
\({R}_{1}\) |
\(2m\) |
Figure 1.1-a: Hollow cylinder cutting and loading
1.2. Material properties#
Young’s module: \(E\mathrm{=}1\mathit{MPa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Law of LEMAITRE:
\(g(\sigma ,\lambda ,T)\mathrm{=}{(\frac{1}{K}\frac{\sigma }{{\lambda }^{\frac{1}{m}}})}^{n}\) with \(\frac{1}{K}\mathrm{=}1\), \(\frac{1}{m}\mathrm{=}0\), \(n\mathrm{=}1\)
Law LEMA_SEUIL:
\(g(\sigma ,\lambda ,T)\mathrm{=}A(\frac{2}{\sqrt{3}}\sigma )\Phi\) with \(A\mathrm{=}\frac{\sqrt{3}}{2}\), \(\Phi \mathrm{=}1\) all over the mesh
\(S\mathrm{=}{10}^{\mathrm{-}10}\)
given the value of the various material parameters, the two laws are absolutely identical and can therefore be compared to the same analytical solution.
1.3. Boundary conditions and loading#
Boundary conditions:
The cylinder is locked at \(\mathit{DY}\) on the \([\mathrm{AB}]\) and \([\mathrm{CD}]\) sides.
Charging:
The cylinder is subjected to internal pressure on \(\mathrm{[}\mathit{DA}\mathrm{]}\mathit{P0}\mathrm{=}1.E\mathrm{-}3\mathit{MPa}\)