1. Reference problem#
1.1. Geometry#
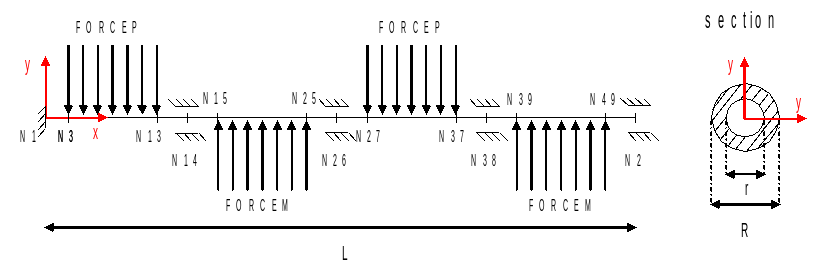
Figure 1.1 Problem geometry and loading system
Geometry of the \((m)\) beam:
\(L=2.436\)
\(R=0.00795\)
\(r=0.00680\)
1.2. Material properties#
Beam
\(E=2.07\mathrm{E11}\mathrm{Pa}\) |
Young’s module |
\(\nu =0.3\) |
Poisson’s ratio |
\(\rho =7870.0{\mathrm{kg.m}}^{-3}\) |
Density |
\(\mathrm{AMOR}\text{\_}\mathrm{ALPHA}\text{}=\text{}1.79E-5{\mathrm{N.s.m}}^{-1}\) |
|
\(\mathrm{AMOR}\text{\_}\mathrm{BETA}\text{}=\text{}0.1526{\mathrm{N.kg}}^{-1}\) |
The coefficients \(\alpha\) and \(\beta\) make it possible to build a viscous damping matrix proportional to stiffness and mass \([C]=\alpha [K]+\beta [M]\)
Obstacles
\(\mathit{RIGI}\text{\_}\mathit{NOR}=1.0E5{\mathit{N.m}}^{-1}\) |
normal stiffness coefficient |
\(\mathrm{AMOR}\text{\_}\mathrm{NOR}=0.28{\mathrm{N.m.s}}^{-1}\) |
normal damping coefficient |
1.3. Boundary conditions and loads#
Imposed displacement:
All nodes on the beam: |
\(\mathrm{DZ}=0\), |
\(\mathrm{DRY}=0\) |
\(\mathrm{DRX}=0\) » |
Node \(\mathrm{N1}\): |
\(\mathrm{DX}=0\), \(\mathrm{DY}=0\), \(\mathrm{DRZ}=0\) |
Imposed load \((N)\):
Knots \(\mathrm{N3}\) to \(\mathrm{N13}\) and \(\mathrm{N27}\) to \(\mathrm{N37}\) |
|
Knots \(\mathrm{N5}\) to \(\mathrm{N25}\) and \(\mathrm{N39}\) to \(\mathrm{N49}\) |
|
with \(\omega =251.2{\mathrm{rad.s}}^{-1}(40\mathrm{Hz})\)
Obstacles located in plane \(Y\) following direction \(y\):
\(\mathrm{N14}\) |
Game = \(0.406E-3m\) |
origin = \((0.609\mathrm{,0}.0\mathrm{,0}.0)\) |
\(\mathrm{N26}\) |
Game = \(0.406E-3m\) |
origin = \((1.218\mathrm{,0}.0\mathrm{,0}.0)\) |
\(\mathrm{N38}\) |
Game = \(0.406E-3m\) |
origin = \((1.827\mathrm{,0}.0\mathrm{,0}.0)\) |
\(\mathrm{N2}\) |
Game = \(0.406E-3m\) |
origin = \((2.436\mathrm{,0}.0\mathrm{,0}.0)\) |