2. Benchmark solution#
2.1. Calculation method#
The reference solution adopted is that obtained by solving the vibrating string equation:
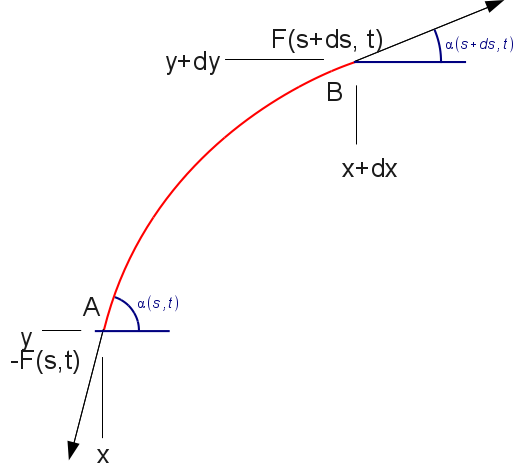
The equation for vibrating strings is:
\(\frac{{\partial }^{2}y}{\partial {t}^{2}}=\frac{{F}_{0}}{\rho S}\frac{{\partial }^{2}y}{\partial {x}^{2}}\)
with:
\({F}_{0}\): tension in the rope,
\(\rho\): density,
\(S\): rope section.
For a string of length \(L\), fixed at these 2 ends, the nth natural vibration frequency is:
\(f=\frac{n}{2L}\sqrt{\frac{{F}_{0}}{\rho S}}\)
2.2. Reference quantities and results#
The quantities tested are the natural vibration frequencies of the cables for 2 calculation moments, which correspond to 2 different voltages.
Not |
Cable Voltage |
Frequency |
10 |
|
|
20 |
|
|
2.3. Uncertainties about the solution#
The solution of the vibrating string equation is obtained under the following hypotheses:
The movements of the rope around its equilibrium position remain small.
the variations in angle \(\alpha\) remain small.
the variation in the tension of the moving rope remains small.
Under these assumptions, the reference solution is free of uncertainty.