1. Reference problem#
1.1. Geometry#
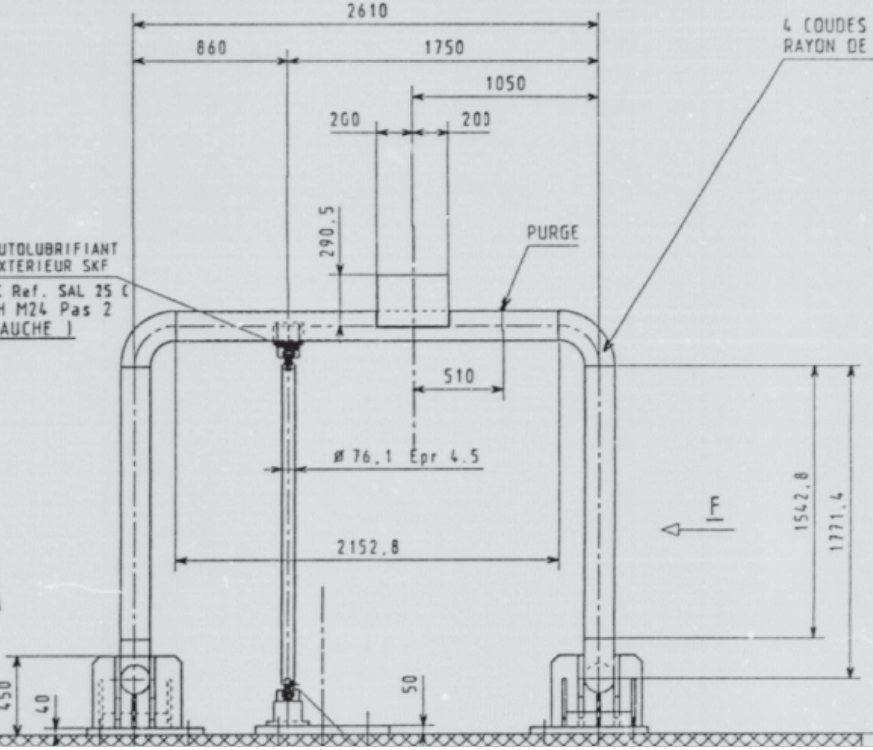
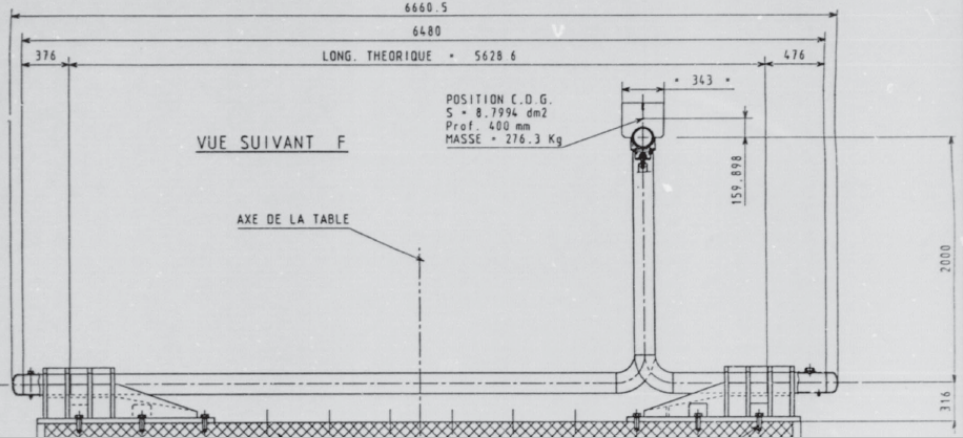
Figure 1.1-a: Geometry (tests ELSA carried out by CEA/EMSI) .
Mesh group:
\(\mathit{POUTRES}\): set of straight pipes
\(\mathit{COUDES}\): set of bent pipes
\(\mathrm{PATVAN},\mathrm{VANNE},\mathrm{ENCBIS1},\mathrm{ENC1},\mathrm{ENC2}\)
\(\mathrm{ENCBIS2},\mathrm{PATBIELA},\mathrm{PATBIELB}\)
\(\mathrm{PATBIELC},\mathrm{BIELA},\mathrm{BIELB},\mathrm{BIELC},\mathrm{CDGVAN}\)
Node group:
\(A,\mathrm{...},L\)
Pipe geometry:
\(\mathit{SECTION}A\)
Mesh groups: \(\mathit{POUTRES}\) \(\mathit{COUDES}\) \(\mathit{PATVAN}\)
\(R=8.485\times {10}^{\text{-2}}m\) Outer radius
\(\mathrm{EP}=7.345\times {10}^{\text{-3}}m\) Thickness
Mesh groups: \(\mathit{BIELA}\), \(\mathrm{BIELB}\), \(\mathrm{BIELC}\)
\(R=38.05\times {10}^{\text{-3}}m\) Outer radius
\(\mathrm{EP}=4.5\times {10}^{\text{-3}}m\) Thickness
\(\mathit{SECTION}B\)
Mesh groups: \(\mathrm{PATBIELC}\)
\(R=4.55\times {10}^{\text{-2}}\) Radius
Mesh groups: \(\mathit{PATBIELA}\)
\(\mathrm{R1}=8.6\times {10}^{\text{-2}}m\) Radius at end 1
\(\mathrm{R2}=4.55\times {10}^{\text{-2}}m\) Radius at end 2
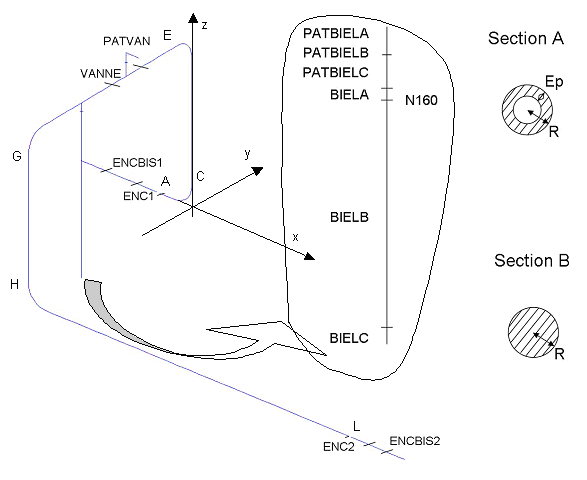
Figure 1.1-b: Geometry modeling.
1.2. Elastic properties of materials#
\(\mathrm{POUTRES}\):
Young’s modulus: \(E=1.9\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Density: \(\rho =1.30273\times {10}^{4}\mathrm{kg}{m}^{\text{-3}}\)
\(\mathrm{COUDE1},\mathrm{COUDE2},\mathrm{COUDE3},\mathrm{COUDE4}\):
Young’s modulus: \(E=1.9\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu =0.3\)
Density: \(\rho =1.47373\times {10}^{4}\mathrm{kg}{m}^{\text{-3}}\)
Slope of the traction curve: \(D\text{\_}\mathrm{SIGM}\text{\_}\mathrm{EPSI}=7.67\times {10}^{9}N{m}^{\text{-2}}\)
Elastic limit: \(\mathit{SY}\mathrm{=}121.2\mathrm{\times }{10}^{6}N{m}^{\text{-2}}\)
Constant of \(\mathrm{PRAGER}\): \(C=5.328434\times {10}^{9}\)
The elastic limit has been reduced in order to plasticize sooner.
\(\mathrm{PATVAN}\):
Young’s modulus: \(E=1.9\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Density: \(\rho =0.0\mathrm{kg}{m}^{\text{-3}}\)
\(\mathrm{PATBIELA}\):
Young’s modulus: \(E=1.8\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Density: \(\rho =4.43\times {10}^{3}\mathrm{kg}{m}^{\text{-3}}\)
\(\mathrm{PATBIELC}\):
Young’s modulus: \(E=1.8\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Density: \(\rho =6.92\times {10}^{3}\mathrm{Kg}/{m}^{3}\)
\(\mathrm{BIELA},\mathrm{BIELB},\mathrm{BIELC}\):
Young’s modulus: \(E=1.8\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Density: \(\rho =6.86\times {10}^{3}\mathrm{kg}{m}^{\text{-3}}\)
\(\mathrm{POUTRES}\):
Young’s modulus: \(E=1.9\times {10}^{11}\mathrm{Pa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
Density: \(\rho =1.47373\times {10}^{4}\mathrm{kg}{m}^{\text{-3}}\)
\(\mathrm{PATBIELB}\) mass added:
\([M]=\left[\begin{array}{ccc}m& 0.& 0.\\ 0.& m& 0.\\ 0.& 0.& m\end{array}\right]\) with \(m=2.46\mathrm{kg}\)
\(\mathrm{CDGVAN}\) (center of gravity of the valve) added mass:
\([M]=\left[\begin{array}{cccccc}m& 0.& 0.& 0.& -{\mathrm{m.e}}_{z}& -{\mathrm{m.e}}_{y}\\ 0.& m& 0.& {\mathrm{m.e}}_{z}& 0.& -{\mathrm{m.e}}_{x}\\ 0.& 0.& m& -{\mathrm{m.e}}_{y}& {\mathrm{m.e}}_{x}& 0.\\ 0.& 0.& 0.& {V}_{\mathrm{xx}}& {V}_{\mathrm{xy}}& {V}_{\mathrm{xz}}\\ 0.& 0.& 0.& 0.& {V}_{\mathrm{yy}}& {V}_{\mathrm{yz}}\\ 0.& 0.& 0.& 0.& 0.& {V}_{\mathrm{zz}}\end{array}\right]\) with \(\begin{array}{c}{V}_{\mathrm{xx}}={I}_{\mathrm{xx}}+m({e}_{y}^{2}+{e}_{z}^{2})\\ {V}_{\mathrm{yy}}={I}_{\mathrm{yy}}+m({e}_{x}^{2}+{e}_{z}^{2})\\ {V}_{\mathrm{zz}}={I}_{\mathrm{zz}}+m({e}_{x}^{2}+{e}_{y}^{2})\\ {V}_{\mathrm{xy}}={I}_{\mathrm{xy}}-{\mathrm{m.e}}_{x}{e}_{y}\\ {V}_{\mathrm{yz}}={I}_{\mathrm{yz}}-{\mathrm{m.e}}_{y}{e}_{z}\\ {V}_{\mathrm{xz}}={I}_{\mathrm{xz}}-{\mathrm{m.e}}_{x}{e}_{z}\end{array}\)
\(m=275\mathrm{kg}\) mass
\(\left[\begin{array}{c}{I}_{\mathrm{xx}}=2.696123\\ {I}_{\mathrm{yy}}=3.81480\text{}\\ \text{}{I}_{\mathrm{zz}}=0.9166667\\ \text{}{I}_{\mathrm{xy}}={I}_{\mathrm{xy}}={I}_{\mathrm{yz}}=0.\end{array}\right]\) mass inertia tensor values
\({e}_{x}={e}_{y}={e}_{z}=0.\) component of the mass eccentricity vector
The non-linearity is due to the material behavior in the bends.
The law of behavior used is: under COMORTEMENT: RELATION =” VMIS_ECMI_LINE “, which corresponds to elastoplasticity with mixed isotropic and linear kinematic work hardening.
1.3. Boundary conditions and loads#
Travel required:
\(\mathrm{ENC1},\mathrm{ENCBIS1}\):
\(\mathit{DX}\mathrm{=}\mathit{DY}\mathrm{=}\mathit{DZ}\mathrm{=}\mathit{DRX}\mathrm{=}\mathit{DRY}\mathrm{=}\mathit{DRZ}\mathrm{=}0\)
\(\mathrm{ENC2},\mathrm{ENCBIS2}\):
\(\mathit{DX}\mathrm{=}\mathit{DY}\mathrm{=}\mathit{DZ}\mathrm{=}\mathit{DRX}\mathrm{=}\mathit{DRY}\mathrm{=}\mathit{DRZ}\mathrm{=}0\)
\(\mathrm{PATBIEL4}\):
\(\mathrm{DX}=\mathrm{DY}=\mathrm{DZ}=\mathrm{DRZ}=0\)
\(\mathit{PATBIEL3}\):
\(\mathit{DRZ}\mathrm{=}0\)
Imposed links:
\(\mathrm{PATVAN},\mathrm{VANNE}\): LIAISON_SOLIDE
\(\mathrm{PATBIEL3},\mathrm{PATBIEL2}\): LIAISON_UNIF (DX, DY, DZ)
Pressure imposed:
\(\mathrm{COUDES},\mathrm{POUTRES}\):
\(\mathit{PRES}\mathrm{=}120.5\mathit{Pa}\)
Seismic loading:
The structure is subjected to seismic loading in direction X. The imposed accelerogram is characterized by a total duration of \(\mathrm{40,95}s\) and a time step of \(\mathrm{0,01}s\).
1.4. Initial conditions and list of calculation times#
The system is initially at rest.
To limit time CPU, we will only conduct the numerical simulation until a final moment worth \(\mathrm{0,17}s\). At this moment, the level of loading reached is such that plasticity has already occurred.
We build a list of optimized calculation times: the time step increasing from \(\mathrm{0,01}s\) to 0.001 s in order to go linear quickly and to reduce the time step just before plasticization.