1. Reference problem#
1.1. Geometry#
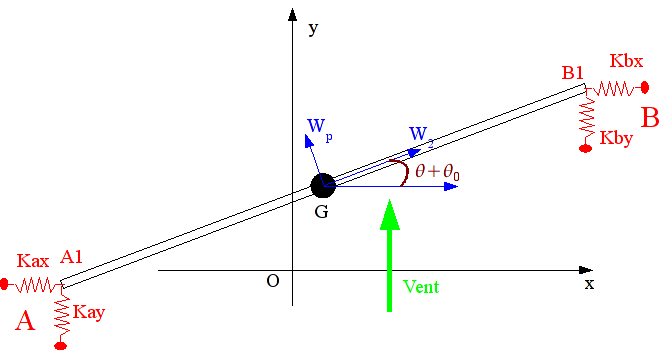
Beam length: \(\mathrm{1.5m}\)
Discreet stiffness: \(\mathrm{kax}\), \(\mathrm{kay}\),, \(\mathrm{kbx}\), \(\mathrm{kby}\)
1.2. Material properties#
Material for the line element: \(E=2.0E+10\), \(\rho =1000.0\)
Mechanical characteristics of the girder: \(\mathrm{section}=\text{'}\mathrm{CERCLE}\text{'}\), \(\mathrm{rayon}=0.1\), \(\mathrm{ep}=0.1\)
The stiffness of the springs:
\(\mathrm{Kxa}\) |
|
|
|
\(10N/m\) |
|
|
|
1.3. Boundary conditions and loads#
At points \(A\) and \(B\): blocking the degrees of freedom: \(\mathrm{DX},\mathrm{DY},\mathrm{DZ}\)
At points \(\mathrm{A1}\) and \(\mathrm{B1}\): blocking the degrees of freedom: \(\mathrm{DZ},\mathrm{DRX},\mathrm{DRY}\)
The springs are modelled by dimensionless discretes. Nodes \(A\) and \(\mathrm{A1}\), \(B\) and \(\mathrm{B1}\) are geometrically confused.
The characteristics of the wind speed field, along axis \(y\):
\(\mathit{Vy}\mathrm{=}\mathrm{20.sin}(\omega \mathrm{.}t)\), with \(\omega =2.\pi \mathrm{.}f\) and \(f=0.2\mathrm{Hz}\)
1.4. Initial conditions#
The beam has an angle of \(30°\) (\({\theta }_{0}=30°\)) with respect to the \(x\) axis.